题目内容
11.已知a、b为任意两个正数,当a、b之间满足什么关系时,等式($\frac{1}{a}$$+\frac{1}{b}$)2=$\frac{4}{ab}$,请说明理由.分析 首先对等号左边括号内的式子通分相加,然后进行平方计算,根据与等号右边的式子相等,即可变形求解.
解答 解:($\frac{1}{a}$$+\frac{1}{b}$)2=$\frac{4}{ab}$,
即($\frac{a+b}{ab}$)2=$\frac{{a}^{2}+2ab+{b}^{2}}{{a}^{2}{b}^{2}}$=$\frac{4}{ab}$,
即$\frac{{a}^{2}+2ab+{b}^{2}}{ab}$=4,
即a2+2ab+b2=4ab,(a-b)2=0,
则当a=b≠0时,等式成立.
点评 本题考查了分式的运算,正确注意到分式有意义的条件:分母≠0是关键.

练习册系列答案
相关题目
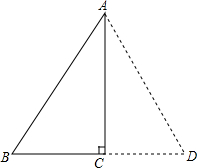 在证明含30°角的直角三角形的性质时,有的同学采用了下面的做法:
在证明含30°角的直角三角形的性质时,有的同学采用了下面的做法: