题目内容
5. 如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点O顺时针旋转90°后得到矩形ABCD.
如图,矩形PMON的边OM,ON分别在坐标轴上,且点P的坐标为(-2,3).将矩形PMON绕点O顺时针旋转90°后得到矩形ABCD.(1)请在图中的直角坐标系中画出旋转后的图形;
(2)若过点P的一条直线恰好将矩形ABCD的面积二等分,求这条直线的解析式.
分析 (1)分别作出点P、M、N绕点O顺时针旋转90°后得到对应点,依次连接即可;
(2)欲将矩形面积等分,直线必过对角线交点,待定系数法求解可得解析式.
解答 解:(1)如图所示,矩形ABCD即为所求作四边形.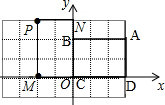
(2)欲将矩形面积等分,直线必过对角线交点,因此直线过(-2,3)和(1.5,1)
设直线解析式为y=kx+b,则
$\left\{\begin{array}{l}{-2k+b=3}\\{1.5k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{4}{7}}\\{b=\frac{13}{7}}\end{array}\right.$,
∴这条直线的解析式是y=-$\frac{4}{7}$x+$\frac{13}{7}$.
点评 本题主要考查旋转变换的作图和矩形性质及待定系数法求函数解析式,熟练掌握旋转变换的定义及矩形的性质是解题的关键.

练习册系列答案
相关题目
16.某市有3000名初一学生参加期末考试,为了了解这些学生的数学成绩,从中抽取200名学生的数学成绩进行统计分析.在这个问题中,下列说法:
①这3000名初一学生的数学成绩的全体是总体;
②每个初一学生是个体;
③200名初一学生是总体的一个样本;
④样本容量是200.
其中说法正确的是( )
①这3000名初一学生的数学成绩的全体是总体;
②每个初一学生是个体;
③200名初一学生是总体的一个样本;
④样本容量是200.
其中说法正确的是( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
13.下列统计中,适宜全面调查的是( )
| A. | 检测某城市的空气质量 | B. | 调查全国初中生的视力情况 | ||
| C. | 审查某篇文章的错别字 | D. | 调查某池塘中现有鱼的数量 |
14.下列调查中,适宜用普查方式的是( )
| A. | 调查高邮市民的吸烟情况 | |
| B. | 调查高邮市民的幸福指数 | |
| C. | 调查高邮市民家族日常生活支出情况 | |
| D. | 调查高邮市某校班级学生对“文明城市”的知晓率 |
 如图,在?ABCD中,点P是AB边上一点(不与A,B重合),CP=CD,过点P作PQ⊥CP,交AD边于点Q,连结CQ.
如图,在?ABCD中,点P是AB边上一点(不与A,B重合),CP=CD,过点P作PQ⊥CP,交AD边于点Q,连结CQ.