题目内容
6.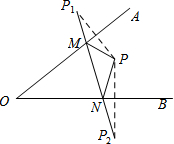 如图所示,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2.连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为6.
如图所示,点P为∠AOB内一点,分别作出点P关于OA、OB的对称点P1、P2.连接P1P2交OA于M,交OB于N,若P1P2=6,则△PMN的周长为6.
分析 根据轴对称的性质可得P1M=PM,PN=P2N,然后求出△PMN的周长=P1P2.
解答 解:∵点P关于OA的对称点P1,
∴OA是PP1的中垂线,
∴P1M=PM,
同理可得:P2N=PN,
∵△PMN的周长=PM+PN+MN,
∴△PMN的周长=P1M+MN+P2N=P1P2=6,
故答案为:6.
点评 本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
相关题目
17.若x=$\root{3}{-2}$,则下列式子正确的是( )
| A. | 3x=-2 | B. | x3=-2 | C. | (-x)3=-2 | D. | x=(-2)3 |
16.下列说法正确的是( )
| A. | 正有理数和负有理数统称为有理数 | |
| B. | 符号不同的两个数互为相反数 | |
| C. | 绝对值等于它的相反数的数是非正数 | |
| D. | 两数相加,和一定大于任何一个加数 |