题目内容
13．
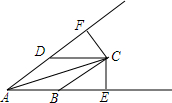如图，点D、B分别在∠A的两边上，过点B作BC∥AD，过点D作DC∥AB交BC于点C，过点C分别作∠A两边的垂线，垂足分别为E、F，若BC=DC，求证：点C在∠A的平分线上．
分析 先证明四边形ABCD是平行四边形，再由已知条件得出平行四边形ABCD是菱形，由菱形的对角线平分一组对角即可得出结论．
解答 证明：∵BC∥AD，DC∥AB，
∴四边形ABCD是平行四边形，
∵BC=DC，
∴平行四边形ABCD是菱形，
∴∠BAC=∠DAC，
即点C在∠BAD的平分线上．
点评 本题考查了平行四边形的判定方法、菱形的判定与性质；熟练掌握菱形的判定与性质，证明四边形是菱形是解决问题的关键．
练习册系列答案
相关题目
4．
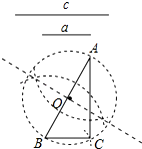数学课上，老师提出如下问题：已知线段a、c，用尺规作图求作直角三角形ABC，使其斜边AB=c，一条直角边BC=a．小明设计了如下的作图步骤：
（1）作线段AB=c；
（2）作线段AB的中点O
（3）以O为圆心，OA长为半径作⊙O
（4）以点B为圆心，线段a的长为半径作弧交⊙O于点C
你认为这种作法中判断∠ACB是直角的依据是（ ）
数学课上，老师提出如下问题：已知线段a、c，用尺规作图求作直角三角形ABC，使其斜边AB=c，一条直角边BC=a．小明设计了如下的作图步骤：（1）作线段AB=c；
（2）作线段AB的中点O
（3）以O为圆心，OA长为半径作⊙O
（4）以点B为圆心，线段a的长为半径作弧交⊙O于点C
你认为这种作法中判断∠ACB是直角的依据是（ ）
| A． | 勾股定理 | B． | 直径所对的圆周角是直角 | ||
| C． | 勾股定理的逆定理 | D． | 90°的圆周角所对的弦是直径 |
1．在平面直角坐标系中，已知点O（0，0）、A（1，$\sqrt{3}$）、B（2，0），点P是线段OB的中点，将△OAB绕点O逆时针旋转30°，记点P的对应点为点Q，则点Q的坐标是（ ）
| A． | （-$\frac{{\sqrt{3}}}{2}$，-$\frac{1}{2}$） | B． | （-$\frac{1}{2}$，-$\frac{{\sqrt{3}}}{2}$） | C． | （$\frac{{\sqrt{3}}}{2}$，$\frac{1}{2}$） | D． | （$\frac{1}{2}$，$\frac{{\sqrt{3}}}{2}$） |
已知∠1和∠2，求作一个角，使它等于∠1与∠2的和．