题目内容
4．
如图，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE交于O，连结AO，则图中共有全等的三角形的对数为（ ）| A． | 2对 | B． | 3对 | C． | 4对 | D． | 5对 |
分析 根据AB=AC，BD⊥AC于D，CE⊥AB于E，∠CAE=∠BAD，可证明△CAE≌△BAD，得出AD=AE，∠C=∠B，根据AAS可证明△DCO≌△EBO，得出CO=BO，利用SSS证得△ACO≌△ABO，利用HL证得△DAO≌△EAO，由此得出共有全等的三角形的对数为4对．
解答 解：由题意可得△CAE≌△BAD，△DCO≌△EBO，△ACO≌△ABO，△DAO≌△EAO共4对三角形全等．
故选：C．
点评 本题考查了全等三角形的判定，判定两个三角形全等的一般方法有：SSS、SAS、ASA、AAS、HL．注意：AAA、SSA不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．
练习册系列答案
相关题目
14．下列说法错误的是（ ）
| A． | 0是最小的整数 | B． | 1是最小的正整数 | C． | 0是最小的自然数 | D． | 自然数是非负数 |
12．如果三角形的三边长分别为m-1，m，m+1（m为正数），则m的取值范围是（ ）
| A． | m＞0 | B． | m＞-2 | C． | m＞2 | D． | m＜2 |
9．
如图，矩形ABCD中，E为CD的中点，连接AE并延长交BC的延长线于点F，连接BD交AF于点H，AB=5，且tan∠EFC=$\frac{{\sqrt{2}}}{4}$，那么AH的长为（ ）
如图，矩形ABCD中，E为CD的中点，连接AE并延长交BC的延长线于点F，连接BD交AF于点H，AB=5，且tan∠EFC=$\frac{{\sqrt{2}}}{4}$，那么AH的长为（ ）| A． | 5 | B． | $5\sqrt{2}$ | C． | 10 | D． | $3\sqrt{6}$ |
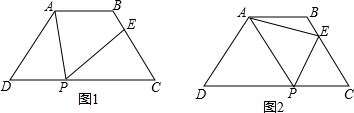
如图，在梯形ABCD中，AD∥BC，AC、BD相交于点E，S△ADE：S△ADC=1：3，那么S△ADE：S△CBE=1：4．