Question

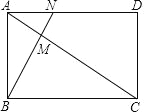
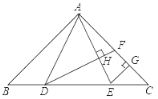
【题目】如图，在△ABC中，AB＝AC，点D、E在线段BC上，且BE＝CD，连接AD、AE，过点D作DF⊥AE，垂足为H，交AC于点F，过点E作EG⊥AC，垂足为G．

（1）若DH＝4，AD＝5，HF＝1，求AF的长；

（2）若∠BAC＝90°，求证：AF＝2CG．

Answer 1

【答案】（1）AF＝；（2）见解析.

【解析】

（1）在Rt△ADH中，根据勾股定理可以求得AH的长，继而在Rt△AHF中，利用勾股定理求得AF长即可；

（2）作DM⊥AC于M，证明△ABE≌△ACD，△DAM≌△AEG，继而可得△GEC是等腰直角三角形，再等腰三角形的性质即可得.

（1）在Rt△ADH中，∵AD＝5，DH＝4，

∴AH＝＝3，

在Rt△AHF中，AF＝；

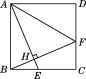
（2）作DM⊥AC于M，

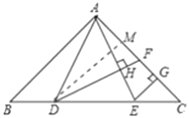
∵AB＝AC，∠BAC＝90°，

∴∠B＝∠C＝45°

∵BE＝CD，

∴△ABE≌△ACD，

∴AD＝AE，∠BAE＝∠CAD，

∴∠CAE＝∠BAD，

∵AE⊥DF，

∴∠AHF＝90°，

∵∠DAF＝90°﹣∠BAD，∠DFA＝90°﹣∠CAE，

∴∠DAF＝∠DFA，

∴DA＝DF，

∴AE＝AD，

∵AB∥DM，∴∠ADM＝∠BAD＝∠EAG，

∵∠AMD＝∠AGE＝90°，

∴△DAM≌△AEG，

∴AM＝GE，

∵∠C＝45°，EG⊥AC，

∴△GEC是等腰直角三角形，

∴EG＝CD，

∵AD＝DF，DM⊥AF，

∴AM＝FM，

∴AF＝2CG．