题目内容
 如图,若△ABC为等腰直角三角形,其中∠ABC=90°,AB=BC=2
如图,若△ABC为等腰直角三角形,其中∠ABC=90°,AB=BC=2| 2 |
考点:圆锥的计算,点、线、面、体
专题:
分析:易得此几何体为圆锥,那么表面积=底面积+侧面积=π×底面半径2+底面周长×母线长÷2.
解答:解:作BF⊥AC,
由题意知,∵在Rt△ABC中,∠ACB=90°,AB=BC=2
cm,
∴AC2=AB2+BC2=16,
∴AC=4,
以BF为半径的圆的周长=2π×2
=4
π,
得到的几何体表面积为
×4
π(AB+BC)=
×4
π×4
=16π.
由题意知,∵在Rt△ABC中,∠ACB=90°,AB=BC=2
| 2 |
∴AC2=AB2+BC2=16,
∴AC=4,

以BF为半径的圆的周长=2π×2
| 2 |
| 2 |
得到的几何体表面积为
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:此题主要考查了圆锥侧面积的计算,关键是利用圆锥的侧面积=底面周长×母线长÷2得出.

练习册系列答案
相关题目
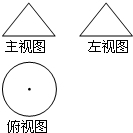 如图,将一个三角形绕其一边旋转一周后得到一个几何体,几何体的主视图和左视图都是边长为1的等边三角形,俯视图是一个圆,那么这个三角形的三条边长分别是多少?
如图,将一个三角形绕其一边旋转一周后得到一个几何体,几何体的主视图和左视图都是边长为1的等边三角形,俯视图是一个圆,那么这个三角形的三条边长分别是多少? 如图,已知数轴上有A、B两个点,它们表示的数分别是-24、-10.现有动点P从A点出发,以每秒3个单位长度的速度向右移动,与此同时,动点Q从B点出发,以每秒2个单位长度的速度向右移动,移动时间为t秒.
如图,已知数轴上有A、B两个点,它们表示的数分别是-24、-10.现有动点P从A点出发,以每秒3个单位长度的速度向右移动,与此同时,动点Q从B点出发,以每秒2个单位长度的速度向右移动,移动时间为t秒.