题目内容
直线y= x+b与双曲线y=
x+b与双曲线y= 交于A(-2,y1)、B(-1,y2),又C(1,y3)在双曲线y=
交于A(-2,y1)、B(-1,y2),又C(1,y3)在双曲线y= 上,则下列结论正确的是
上,则下列结论正确的是
- A.y1>y2>y3
- B.y3>y1>y2
- C.y2>y1>y3
- D.y3>y2>y1
D
分析:由直线y= x+b与双曲线y=
x+b与双曲线y= 交于A(-2,y1)、B(-1,y2),根据一次函数与反比例函数的增减性,可确定k>0且0>y2>y1,又由C(1,y3)在双曲线y=
交于A(-2,y1)、B(-1,y2),根据一次函数与反比例函数的增减性,可确定k>0且0>y2>y1,又由C(1,y3)在双曲线y= 上,可得y3>0,继而求得答案.
上,可得y3>0,继而求得答案.
解答:∵ >0,
>0,
∴直线y= x+b中,y随x的增大而增大,
x+b中,y随x的增大而增大,
∵A(-2,y1)、B(-1,y2)在直线y= x+b上,
x+b上,
∴y2>y1,
∵A(-2,y1)、B(-1,y2)在双曲线y= 上,
上,
∴k>0,
∴0>y2>y1,
∵C(1,y3)在双曲线y= 上,
上,
∴y3>0,
∴y3>y2>y1.
故选D.
点评:此题考查了反比例函数与一次函数的增减性.此题难度适中,注意掌握反比例函数与一次函数的性质是解此题的关键.
分析:由直线y=
 x+b与双曲线y=
x+b与双曲线y= 交于A(-2,y1)、B(-1,y2),根据一次函数与反比例函数的增减性,可确定k>0且0>y2>y1,又由C(1,y3)在双曲线y=
交于A(-2,y1)、B(-1,y2),根据一次函数与反比例函数的增减性,可确定k>0且0>y2>y1,又由C(1,y3)在双曲线y= 上,可得y3>0,继而求得答案.
上,可得y3>0,继而求得答案.解答:∵
 >0,
>0,∴直线y=
 x+b中,y随x的增大而增大,
x+b中,y随x的增大而增大,∵A(-2,y1)、B(-1,y2)在直线y=
 x+b上,
x+b上,∴y2>y1,
∵A(-2,y1)、B(-1,y2)在双曲线y=
 上,
上,∴k>0,
∴0>y2>y1,
∵C(1,y3)在双曲线y=
 上,
上,∴y3>0,
∴y3>y2>y1.
故选D.
点评:此题考查了反比例函数与一次函数的增减性.此题难度适中,注意掌握反比例函数与一次函数的性质是解此题的关键.

练习册系列答案
相关题目
 x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+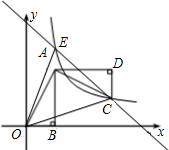 绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y=
绕点A逆时针旋转90°,点O的对应点C恰好落在双曲线y= 如图,直线y=mx+n与双曲线y=
如图,直线y=mx+n与双曲线y= 如图,直线y=-2x-2与双曲线
如图,直线y=-2x-2与双曲线 如图,直线y1=mx+n与双曲线
如图,直线y1=mx+n与双曲线