题目内容
已知abc≠0且a+b+c=0，则a（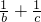
）+b（
）+c（
）的值为
- A.0
- B.1
- C.-1
- D.-3
D
分析：先利用乘法的分配律得到原式=
+
+
+
+
+
，再把同分母相加，然后根据abc≠0且a+b+c=0得到a+c=-b，b+c=-a，a+b=-c，把它们代入即可得到原式的值．
解答：原式=+++++
=
+
+
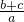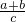
∵abc≠0且a+b+c=0，
∴a+c=-b，b+c=-a，a+b=-c，
∴原式=-1-1-1=-3．
故选D．
点评：本题考查了分式的化简求值：先把分式根据已知条件进行变形，然后利用整体代入的方法进行化简、求值．
分析：先利用乘法的分配律得到原式=
+++++，再把同分母相加，然后根据abc≠0且a+b+c=0得到a+c=-b，b+c=-a，a+b=-c，把它们代入即可得到原式的值．解答：原式=
+++++=
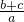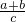
++∵abc≠0且a+b+c=0，
∴a+c=-b，b+c=-a，a+b=-c，
∴原式=-1-1-1=-3．
故选D．
点评：本题考查了分式的化简求值：先把分式根据已知条件进行变形，然后利用整体代入的方法进行化简、求值．
练习册系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
如图，已知△ABC，且S△ABC=1，D、E分别是AB、AC上的动点，BD与CE相交于点P，使SBCDE=
（2012•贵港）如图，已知△ABC，且∠ACB=90°．
