题目内容
【题目】已知:![]() 为
为![]() 的直径,弦
的直径,弦![]() 于点
于点![]() ,连接
,连接![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 并延长
并延长![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
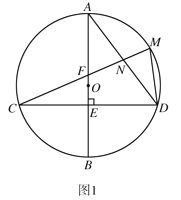
(1)如图1,连接![]() .求证:
.求证:![]() ;
;
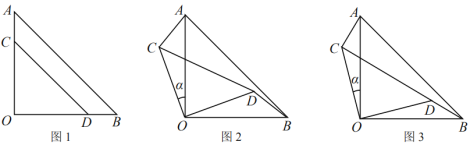
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 延长线于点
延长线于点![]() 求证:
求证:![]() .
.
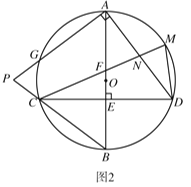
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由垂径定理和圆周角定理进行等量转换即可得证;
(2)由圆周角定理和全等三角形的性质进行等量转换,即可得解;
(3)利用圆周角定理和三角函数进行等量转换,即可得解.
(1)连接![]() ,如图所示
,如图所示
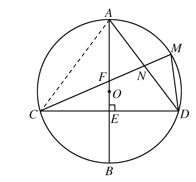
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵弧![]() 弧
弧![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() .
.
(2)连接![]() ,
,![]() ,如图所示
,如图所示
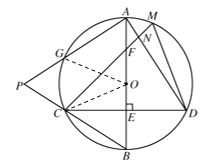
∵OG为半径,![]()
∴![]() ,
,
∴ ![]() ,
,
∵弧![]() 弧
弧![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵OA=OG=OC=OB
∴∠AOG=∠BOC
∴![]()
∴![]() ,
,
∴![]() ,
,
即![]() .
.
(3)∵弧CD=2弧CB
∴![]()
∴![]() ,
,
∵![]() ,CF=FD
,CF=FD
∴![]() ,
,
∴FD⊥MF
∴![]() ,
,
∴![]()
设![]() ,
,![]()
∵![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,![]() ,
,
∵∠CAB=∠DAB
∴![]()
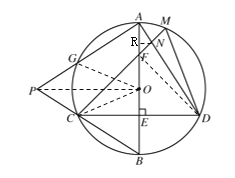
作![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
连接![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目