题目内容
20.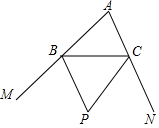 如图,△ABC的外角∠MBC,∠NCB的平分线交于P,求证:点P在∠BAC的平分线上.
如图,△ABC的外角∠MBC,∠NCB的平分线交于P,求证:点P在∠BAC的平分线上.
分析 首先过点P作PD⊥AM于点D,作PE⊥BC于点E,作PF⊥AN于点F,由BP、CP分别是ABC的外角∠CBD、∠BCE的平分线,根据角平分线的性质,易证得PD=PE=PF,又由在角内部,且到角两边距离相等的点,在此角的平分线上,证得P点在∠BAC的平分线上.
解答 证明:过点P作PD⊥AM于点D,作PE⊥BC于点E,作PF⊥AN于点F,
∵BP、CP分别是ABC的外角∠CBD、∠BCE的平分线,
∴PD=PE,PF=PE,
∴PD=PF,
∴P点在∠BAC的平分线上
点评 此题考查了角平分线的性质与判定.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.用反证法证明命题:在一个三角形中,最大的内角不小于60°,证明的第一步是( )
| A. | 假设最大的内角小于60° | B. | 假设最大的内角大于60° | ||
| C. | 假设最大的内角大等于60° | D. | 假设最大的内角小等于60° |
12.用反证法证明“若a>b>0,则a2>b2”,应假设( )
| A. | a2<b2 | B. | a2=b2 | C. | a2≤b2 | D. | a2≥b2 |
8.以x为未知数的方程$\frac{s}{x}$=$\frac{s+40}{x+v}$(s>0,v>0)的解为( )
| A. | x=$\frac{sv}{40}$ | B. | x=$\frac{sv}{50}$ | C. | x=$\frac{s+v}{40}$ | D. | x=$\frac{s-v}{40}$ |
 若抛物线L:y=ax2+bx+c(a,b,c是常数,且abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称此抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.
若抛物线L:y=ax2+bx+c(a,b,c是常数,且abc≠0)与直线l都经过y轴上的同一点,且抛物线L的顶点在直线l上,则称此抛物线L与直线l具有“一带一路”关系,并且将直线l叫做抛物线L的“路线”,抛物线L叫做直线l的“带线”.