题目内容
19.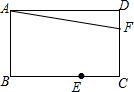 在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,若AD=$\sqrt{3}$AB=3,则S△ADF=( )
在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,若AD=$\sqrt{3}$AB=3,则S△ADF=( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}-\frac{15}{2}$ | C. | 3$\sqrt{3}$$-\frac{9}{2}$ | D. | $\frac{9}{2}$ |
分析 由AD=$\sqrt{3}$AB=3,可求得AB=$\sqrt{3}$,AD=3,又由在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,根据轴对称的性质,可求得BE,CF的长,继而求得DF的长,于是求得答案.
解答 解:∵AD=$\sqrt{3}$AB=3,
∴AB=$\sqrt{3}$,AD=3,
∵四边形ABCD是矩形,
∴BC=AD=3,CD=AB=$\sqrt{3}$,
∵在矩形ABCD中,点A关于角B的角平分线的对称点为E,点E关于角C的角平分线的对称点为F,
∴BE=AB=$\sqrt{3}$,
∴CF=CE=BC-BE=3-$\sqrt{3}$,
∴DF=CD-CF=2$\sqrt{3}$-3,
∴S△ADF=$\frac{1}{2}$AD•DF=$\frac{1}{2}$×3×(2$\sqrt{3}$-3)=3$\sqrt{3}$-$\frac{9}{2}$.
故选C.
点评 此题考查了矩形的性质、轴对称的性质,三角形面积的计算,勾股定理.注意掌握轴对称图形的对应关系.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
7.多项式x2y-xy2+3xy-1的次数与常数项分别是( )
| A. | 2,-1 | B. | 3,1 | C. | 3,-1 | D. | 2,1 |
14.已知单项式4x3ym与-3xn-1y3的和是单项式,则这两个单项式的和是( )
| A. | x2y3 | B. | x3y2 | C. | xn-1ym | D. | xn+2ym+2 |
4. 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )
 如图,笑脸盖住的点的坐标可能为( )
如图,笑脸盖住的点的坐标可能为( )| A. | (2,3) | B. | (-2,3) | C. | (-2,-3) | D. | (2,-3) |
8.下列说法属于不可能事件的是( )
| A. | 四边形的内角和为360° | B. | 对角线相等的菱形是正方形 | ||
| C. | 内错角相等 | D. | 存在实数x满足x2+1=0 |
 如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断:
如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为MN(点M、N分别在边AC、BC上),给出以下判断: