题目内容
方程x2+mx-2n=0的两个根分别为2和-5，则m=________，n=________．
3 5
分析：由一元二次方程根与系数关系列出方程组
，通过解该方程组即可求得m、n的值．
解答：∵方程x2+mx-2n=0的两个根分别为2和-5，
∴由一元二次方程根与系数关系，有：，
解得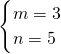
．
故答案是：3，5．
点评：本题考查了一元二次方程的根与系数的关系．若x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1•x2=q．
分析：由一元二次方程根与系数关系列出方程组
，通过解该方程组即可求得m、n的值．解答：∵方程x2+mx-2n=0的两个根分别为2和-5，
∴由一元二次方程根与系数关系，有：
，解得
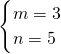．故答案是：3，5．
点评：本题考查了一元二次方程的根与系数的关系．若x1，x2是方程x2+px+q=0的两根时，x1+x2=-p，x1•x2=q．
练习册系列答案
相关题目
若m、n都是正实数，方程x2+mx+2n=0和方程x2+2nx+m=0都有实数根，则m+n的最小值是（ ）
| A、4 | B、6 | C、8 | D、10 |