题目内容
18.解方程组:(1)$\left\{\begin{array}{l}{x+y=3}\\{x+z=5}\\{y+z=6}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+y+z=-1}\\{3y-z=-1}\\{3x+2y+3z=-5}\end{array}\right.$.
分析 (1)方程组三个方程相加求出x+y+z的值,将三个方程代入依次求出x,y,z的值即可;
(2)方程组利用加减消元法求出解即可.
解答 解:(1)$\left\{\begin{array}{l}{x+y=3①}\\{x+z=5②}\\{y+z=6③}\end{array}\right.$,
①+②+③得:2(x+y+z)=14,即x+y+z=7④,
把①代入④得:z=4;
把②代入④得:y=2;
把③代入④得:x=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=2}\\{z=4}\end{array}\right.$;
(2)$\left\{\begin{array}{l}{2x+y+z=-1①}\\{3y-z=-1②}\\{3x+2y+3z=-5③}\end{array}\right.$,
①×3-③×2得:-y-3z=7④,
③+④×3得:-10z=20,即z=-2,
把z=-2代入④得:y=-1,
把z=-2,y=-1代入①得:x=1,
则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\\{z=-2}\end{array}\right.$.
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
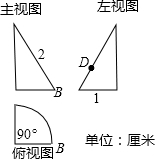 如图是一个锥体的三视图.
如图是一个锥体的三视图. 用6个完全相同菱形拼成如图所示的图案,则菱形中较大的内角度数为120°.
用6个完全相同菱形拼成如图所示的图案,则菱形中较大的内角度数为120°. 已知,在Rt△ABC中,∠ACB=90°,P是AC的中点.
已知,在Rt△ABC中,∠ACB=90°,P是AC的中点.