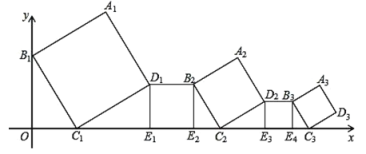
题目内容
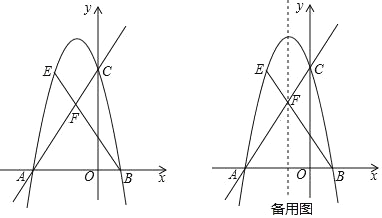
【题目】如图,在平面直角坐标系中,![]() ,
,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 轴上的点,且
轴上的点,且![]() ,
,![]() ,
,![]() 为线段
为线段![]() 的中点,
的中点,![]() ,
,![]() 为
为![]() 轴正半轴上的任意一点,连结
轴正半轴上的任意一点,连结![]() ,以
,以![]() 为边按顺时针方向作正方形
为边按顺时针方向作正方形![]() .
.

(1)填空:点![]() 的坐标为______;
的坐标为______;
(2)记正方形![]() 的面积为
的面积为![]() ,①求
,①求![]() 关于
关于![]() 的函数关系式;②当
的函数关系式;②当![]() 时,求
时,求![]() 的值.
的值.
(3)是否存在满足条件的![]() 的值,使正方形的顶点
的值,使正方形的顶点![]() 或
或![]() 落在
落在的边上?若存在,求出所有满足条件的
![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1)![]() .(2)①
.(2)①![]() .②
.②![]() .(3)
.(3)![]() ,21,3,
,21,3,![]() .
.
【解析】
(1)根据点C的坐标和正弦的定义即可求出AC,利用勾股定理即可求出OA,从而求出结论;
(2)①过点![]() 作
作![]() 轴于点
轴于点![]() ,易证DH为
,易证DH为![]() 的中位线,根据三角形中位线的性质可得
的中位线,根据三角形中位线的性质可得![]() ,
,![]() ,
,![]() ,然后根据正方形的面积公式和勾股定理即可求出结论;
,然后根据正方形的面积公式和勾股定理即可求出结论;
②易知此时点![]() 即为正方形
即为正方形![]() 的中心,从而得出
的中心,从而得出![]() ,从而求出a的值,结合①的结论即可求出S;
,从而求出a的值,结合①的结论即可求出S;
(3)根据点F和点G落在![]() 的各边分类讨论,分别画出对应的图形,根据全等三角形的判定及性质、相似三角形的判定及性质即可分别求出结论.
的各边分类讨论,分别画出对应的图形,根据全等三角形的判定及性质、相似三角形的判定及性质即可分别求出结论.
解:(1)∵![]() ,
,![]()
∴OC=8,![]()
解得:AC=10
根据勾股定理可得OA=![]()
∵点A在x轴负半轴上
∴![]()
故答案为:![]() .
.
(2)①如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
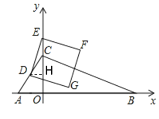
∵![]() 为线段
为线段![]() 的中点,DH⊥y轴,AO⊥y轴
的中点,DH⊥y轴,AO⊥y轴
∴DH∥AO
∴DH为![]() 的中位线
的中位线
∴![]() ,
,![]()
∴![]() ,
,
∴![]() .
.
②当![]() 时,点
时,点![]() 即为正方形
即为正方形![]() 的中心,
的中心,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)①当点![]() 落在
落在![]() 边上时,如图,过点D作DM⊥y轴于M,过点F作FN⊥y轴于N
边上时,如图,过点D作DM⊥y轴于M,过点F作FN⊥y轴于N
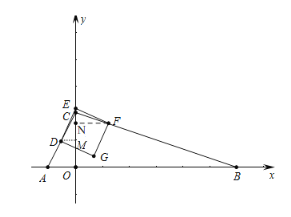
∴∠EMD=∠FNE=90°
∵四边形DGFE为正方形
∴ED=FE,∠DEF=90°
∴∠DEM+∠FEN=90°,∠EFN+∠FEN=90°
∴∠DEM=∠EFN
∴![]() ≌
≌![]()
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∵FN平行OB
∴![]() ∽
∽![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
②当点![]() 落在
落在![]() 边上时,如图,过点D作DM⊥y轴于M,过点G作GQ⊥x轴于Q,QG的延长线于DM的延长线交于点N
边上时,如图,过点D作DM⊥y轴于M,过点G作GQ⊥x轴于Q,QG的延长线于DM的延长线交于点N

∴∠EMD=∠DNG=90°
∵四边形DGFE为正方形
∴ED=DG,∠EDG=90°
∴∠DEM+∠EDN=90°,∠GDN+∠EDN =90°
∴∠DEM=∠GDN
∴![]() ≌
≌![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴tanB=![]()
∴![]()
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() .
.
③当点![]() 落在
落在![]() 边上时,如图,过点D作DM⊥y轴于点M
边上时,如图,过点D作DM⊥y轴于点M
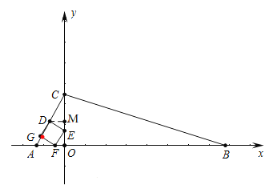
∴∠EMD=∠FOE=90°
∵四边形DGFE为正方形
∴ED=FE,∠DEF=90°
∴∠DEM+∠FEO=90°,∠EFO+∠FEO=90°
∴∠DEM=∠EFO
∴![]() ≌
≌![]()
∴![]() ,即
,即![]() .
.
④当点![]() 落在
落在![]() 边上时,如图,
边上时,如图,
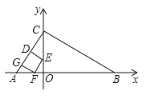
∵∠CDE=∠COA=90°,∠DCE=∠OCA
∴![]() ∽
∽![]()
∴![]() ,
,
∴![]() ,
,
得![]() .
.
综上,所有满足条件的![]() 的值有四个:
的值有四个:![]() ,21,3,
,21,3,![]() .
.