题目内容
12.如图1,在平面直角坐标系xOy中,抛物线y=ax2+1经过点A(4,-3),顶点为点B,点P为抛物线上的一个动点,l是过点(0,2)且垂直于y轴的直线,过P作PH⊥l,垂足为H,连接PO.(1)求抛物线的解析式,并写出其顶点B的坐标;
(2)①当P点运动到A点处时,计算:PO=5,PH=5,由此发现,PO=PH(填“>”、“<”或“=”);
②当P点在抛物线上运动时,猜想PO与PH有什么数量关系,并证明你的猜想;
(3)如图2,设点C(1,-2),问是否存在点P,使得以P,O,H为顶点的三角形与△ABC相似?若存在,求出P点的坐标;若不存在,请说明理由.

分析 (1)利用待定系数法即可解决问题.
(2)①求出PO、PH即可解决问题.
②结论:PO=PH.设点P坐标(m,-$\frac{1}{4}$m2+1),利用两点之间距离公式求出PH、PO即可解决问题.
(3)首先判断PH与BC,PO与AC是对应边,设点P(m,-$\frac{1}{4}$m2+1),由$\frac{PH}{HO}$=$\frac{BC}{BA}$列出方程即可解决问题.
解答 (1)解:∵抛物线y=ax2+1经过点A(4,-3),
∴-3=16a+1,
∴a=-$\frac{1}{4}$,
∴抛物线解析式为y=-$\frac{1}{4}$x2+1,顶点B(0,1).
(2)①当P点运动到A点处时,∵PO=5,PH=5,
∴PO=PH,
故答案分别为5,5,=.
②结论:PO=PH.
理由:设点P坐标(m,-$\frac{1}{4}$m2+1),
∵PH=2-(-$\frac{1}{4}$m2+1)=$\frac{1}{4}$m2+1
PO=$\sqrt{{m}^{2}+(-\frac{1}{4}{m}^{2}+1)^{2}}$=$\frac{1}{4}$m2+1,
∴PO=PH.
(3)∵BC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,AC=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,AB=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$
∴BC=AC,
∵PO=PH,
又∵以P,O,H为顶点的三角形与△ABC相似,
∴PH与BC,PO与AC是对应边,
∴$\frac{PH}{HO}$=$\frac{BC}{BA}$,设点P(m,-$\frac{1}{4}$m2+1),
∴$\frac{\frac{1}{4}{m}^{2}+1}{\sqrt{{m}^{2}+4}}$=$\frac{\sqrt{10}}{4\sqrt{2}}$,
解得m=±1,
∴点P坐标(1,$\frac{3}{4}$)或(-1,$\frac{3}{4}$).
点评 本题考查二次函数综合题、待定系数法、相似三角形的判定和性质等知识,解题的关键是记住两点之间的距离公式,学会转化的思想,用方程去解决问题,属于中考压轴题.

 阅读快车系列答案
阅读快车系列答案| A. | a-c>b-c | B. | c-a>c-b | C. | ac>bc | D. | $\frac{a}{c}$>$\frac{b}{c}$ |
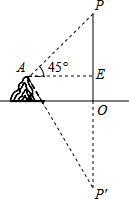 在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )
在湖边高出水面50 m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°.则飞艇离开湖面的高度( )| A. | $25\sqrt{3}+75$ | B. | $50\sqrt{3}+50$ | C. | $75\sqrt{3}+75$ | D. | $50\sqrt{3}+100$ |
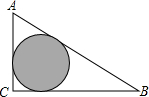 如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )
如图,△ABC是一块绿化带,将阴影部分修建为花圃,已知AB=15,AC=9,BC=12,阴影部分是△ABC的内切圆,一只自由飞翔的小鸟将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{5}$ |
| A. | 0.245×104 | B. | 2.45×103 | C. | 24.5×102 | D. | 2.45×1011 |
| A. | 3 | B. | 2 | C. | 1 | D. | -1 |
 如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论: 如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.
如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,点O在AB上,以点O为圆心,OA为半径的圆恰好经过点D,分别交AC,AB于点E,F.