题目内容
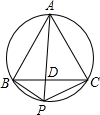如图，已知圆内接等边△ABC，在劣弧BC上有一点P．若AP与BC交于点D，且PB=21，PC=28，则PD=分析：延长BP至E，使PE=PC，连接CE，先判断出△PCE是等边三角形，再判断出PD∥CE，由平行线的性质即可得出答案．
解答：
解：延长BP至E，使PE=PC，连接CE，
∵∠CPE=∠BAC=60°，
∴△PCE是等边三角形，
∴∠PCE=60°=∠APC，
PE=CE=PC=28，
∴PD∥CE，
∴
=
，
∴
=
，
∴PD=12，
解得，DP=12．
故答案为：12．
解：延长BP至E，使PE=PC，连接CE，∵∠CPE=∠BAC=60°，
∴△PCE是等边三角形，
∴∠PCE=60°=∠APC，
PE=CE=PC=28，
∴PD∥CE，
∴
| PD |
| CE |
| BP |
| BE |
∴
| PD |
| 28 |
| 21 |
| 21+28 |
∴PD=12，
解得，DP=12．
故答案为：12．
点评：本题综合考查了相似三角形的判定与性质及全等三角形的性质与判定．
练习册系列答案
相关题目
如图，已知圆内接等边△ABC，在劣弧BC上有一点P．若AP与BC交于点D，且PB=21，PC=28，则PD=________．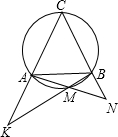
如图，已知等边△ABC内接于圆，在劣弧AB上取异于A、B的点M，设直线AC与BM相交于K，直线CB与AM相交于点N，
