题目内容
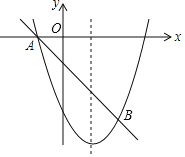
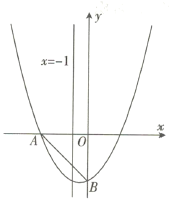
【题目】如图，抛物线
与
轴的负半轴交于点
，与
轴交于点
，连接
，点
分别是直线
与抛物线上的点，若点
围成的四边形是平行四边形，则点
的坐标为__________.
【答案】
或
或
【解析】
根据二次函数
与x轴的负半轴交于点
，与
轴交于点
.直接令x=0和y=0求出A，B的坐标.再根据平行四边形的性质分情况求出点E的坐标.
由抛物线的表达式求得点
的坐标分别为
.
由题意知当
为平行四边形的边时，
，且
，
∴线段
可由线段平移得到.
∵点
在直线
上，①当点的对应点为
时，如图，需先将向左平移1个单位长度，
此时点的对应点
的横坐标为
，将
代入
，
得
，∴
.
②当点A的对应点为
时，同理，先将向右平移2个单位长度，可得点的对应点
的横坐标为2，
将
代入得
，∴
当为平行四边形的对角线时，可知的中点坐标为
，
∵
在直线上，
∴根据对称性可知
的横坐标为
，将
代入
得
，∴
.
综上所述，点
的坐标为或
或
.
练习册系列答案
阅读快车系列答案
相关题目
