题目内容
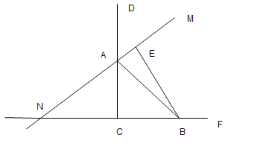
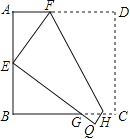
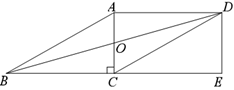
【题目】如图正方形![]() 的顶点
的顶点![]() 是
是![]() 和
和![]() 上的动点,与
上的动点,与![]() 交于P、Q两点,
交于P、Q两点,![]() .
.
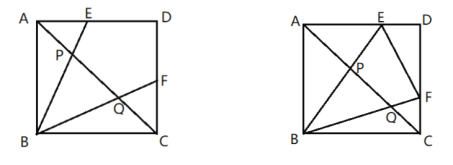
(1)当![]() 时,
时,
①求![]() 的度数;
的度数;
②求以![]() 为边长的正方形面积;
为边长的正方形面积;
(2)当![]() 在
在![]() 上运动时,始终保持
上运动时,始终保持![]() ,连接
,连接![]() ,则
,则![]() 面积的最小值为 (直接写出答案).
面积的最小值为 (直接写出答案).
【答案】(1)①![]() ,②以
,②以![]() 为边的正方形面积为
为边的正方形面积为![]() ;(2)
;(2)![]() .
.
【解析】
(1)根据正方形性质得出![]() ,
,![]() ,由此得知
,由此得知![]() ,然后根据AB=AQ=CP,结合等腰三角形性质以及三角形内角和定理进一步求出答案即可;
,然后根据AB=AQ=CP,结合等腰三角形性质以及三角形内角和定理进一步求出答案即可;
(2)首先根据勾股定理求出![]() ,由此得出
,由此得出![]() ,通过证明
,通过证明![]() 进一步得出
进一步得出![]() ,据此即可得出答案;
,据此即可得出答案;
(3)延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,先证明
,先证明![]() 与
与![]() 全等,得出∠GBF=∠EBF,再证明
全等,得出∠GBF=∠EBF,再证明![]() 与
与![]() 全等,从而得出
全等,从而得出![]() ,即当
,即当![]() 时,
时,![]() 取得最小值,设此时
取得最小值,设此时![]() ,则
,则![]() ,根据题意利用勾股定理得出
,根据题意利用勾股定理得出![]() ,最后得出
,最后得出![]() ,
,![]() ,据此进一步求解即可.
,据此进一步求解即可.
(1)①∵四边形![]() 为正方形,
为正方形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵AB=AQ=CP,
∴AB=AQ=CP=BC,
∴![]() ,
,
同理![]() ,
,
∴![]() ;
;
②∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
故以![]() 为边的正方形面积为
为边的正方形面积为![]() ;
;
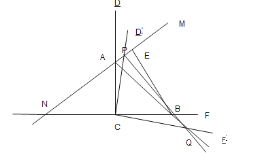
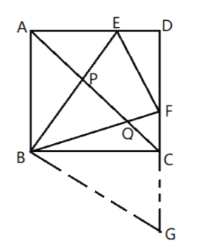
(2)如图,延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() ,
,
在![]() 与
与![]() 中,
中,
∵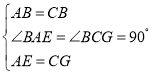
∴![]()
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴∠GBF=∠EBF,
在![]() 与
与![]() 中,
中,
∵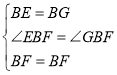
∴![]()
∴![]() ,
,
在![]() 中,
中,![]() ,
,
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() ,
,
设此时![]() ,则
,则![]() ,
,
![]()
由![]() 得:
得:![]()
即![]()
解得![]() (舍去),
(舍去),
∴![]() ,
,![]() ,
,
∴![]() 面积的最小值=
面积的最小值=![]() ,
,
故答案为:![]() .
.

练习册系列答案
相关题目