Question

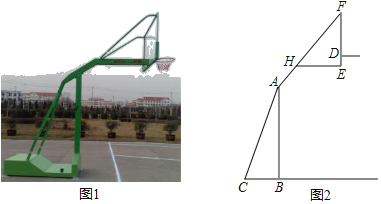
【题目】如图1，2分别是某款篮球架的实物图与示意图，AB⊥BC于点B，底座BC＝1.3米，底座BC与支架AC所成的角∠ACB＝60°，点H在支架AF上，篮板底部支架EH∥BC．EF⊥EH于点E，已知AH＝米，HF＝米，HE＝1米．

（1）求篮板底部支架HE与支架AF所成的∠FHE的度数．

（2）求篮板底部点E到地面的距离，（精确到0.01米）（参考数据：≈1.41，≈1.73）

Answer 1

【答案】（1）45°；（2）2.75米

【解析】

（1）由cos∠FHE＝＝可得答案；

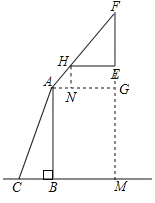
（2）延长FE交CB的延长线于M，过点A作AG⊥FM于G，过点H作HN⊥AG于N，据此知GM＝AB，HN＝EG，Rt△ABC中，求得AB＝BCtan60°＝1.3；Rt△ANH中，求得HN＝AHsin45°＝；根据EM＝EG+GM可得答案．

解：（1）在Rt△EFH中，cos∠FHE＝＝＝，

∴∠FHE＝45°．

答：篮板底部支架HE与支架AF所成的角∠FHE的度数为45°；

（2）延长FE交CB的延长线于M，过点A作AG⊥FM于G，过点H作HN⊥AG于N，

则四边形ABMG和四边形HNGE是矩形，

∴GM＝AB，HN＝EG，

在Rt△ABC中，∵tan∠ACB＝，

∴AB＝BCtan60°＝1.3×＝1.3（米），

∴GM＝AB＝1.3（米），

在Rt△ANH中，∠FAN＝∠FHE＝45°，

∴HN＝AHsin45°＝×＝（米），

∴EM＝EG+GM＝+1.3≈2.75（米）．

答：篮板底部点E到地面的距离大约是2.75米．

故答案为：（1）45°；（2）2.75米．