题目内容
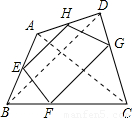
(1999•黄冈)在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的一点,且 =k(k>0).阅读下段材料,回答下列问题:
=k(k>0).阅读下段材料,回答下列问题:如图,连接BD,∵
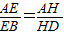 ,∴EH∥BD,∵
,∴EH∥BD,∵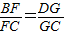 ,∴FG∥BD,∴FG∥EH.
,∴FG∥BD,∴FG∥EH.(1)连接AC,则EF与GH是否一定平行,答:______;
(2)当k值为______时,四边形EFGH为平行四边形;
(3)在(2)的情形下,对角线AC与BD只须满足______条件时,EFGH为矩形;
(4)在(2)的情形下,对角线AC与BD只须满足______条件时,EFGH为菱形.
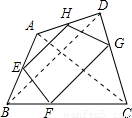
【答案】分析:(1)当E,F,G,H分别是AB,BC,CD,DA的中点时,EF与GH一定平行;
(2)要使四边形EFGH为平行四边形,E,F,G,H必须分别是AB,BC,CD,DA的中点;
(3)要使平行四边形EFGH为矩形,则对角线AC与BD必须垂直,
(3)要使平行四边形EFGH为菱形,则对角线AC与BD必须相等.
解答:解:(1)∵E,F,G,H分别是AB,BC,CD,DA上的一点,∴EH与AC,FG与AC都不一定平行,EF与GH不一定平行;
(2)∵四边形EFGH为平行四边形,
∴EF∥GH,
∴ ,
,
∵ ,
,
∴BF=CF,
∴k=1;
(3)当AC⊥BD时,EFGH为矩形.
由(2)得:四边形OMHN是平行四边形,
∴∠H=∠MON=90°,
∴平行四边形EFGH为矩形;
(4)当AC=BD时,
∵EH=GF= BD,EF=GH=
BD,EF=GH= AC,
AC,
∴EF=FG=GH=EH,
∴四边形EFGH为菱形.
点评:掌握特殊平行四边形的判定是解此题的关键.
(2)要使四边形EFGH为平行四边形,E,F,G,H必须分别是AB,BC,CD,DA的中点;
(3)要使平行四边形EFGH为矩形,则对角线AC与BD必须垂直,
(3)要使平行四边形EFGH为菱形,则对角线AC与BD必须相等.
解答:解:(1)∵E,F,G,H分别是AB,BC,CD,DA上的一点,∴EH与AC,FG与AC都不一定平行,EF与GH不一定平行;
(2)∵四边形EFGH为平行四边形,
∴EF∥GH,
∴
 ,
,∵
 ,
,∴BF=CF,
∴k=1;
(3)当AC⊥BD时,EFGH为矩形.
由(2)得:四边形OMHN是平行四边形,

∴∠H=∠MON=90°,
∴平行四边形EFGH为矩形;
(4)当AC=BD时,
∵EH=GF=
 BD,EF=GH=
BD,EF=GH= AC,
AC,∴EF=FG=GH=EH,
∴四边形EFGH为菱形.
点评:掌握特殊平行四边形的判定是解此题的关键.

练习册系列答案
相关题目
 x2+3mx+18m2-m与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C(0,b),O为原点.
x2+3mx+18m2-m与x轴交于A(x1,0)、B(x2,0)(x1<x2)两点,与y轴交于点C(0,b),O为原点.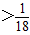 ,且OA+OB=3OC,求抛物线解析式及A,B,C的坐标;
,且OA+OB=3OC,求抛物线解析式及A,B,C的坐标;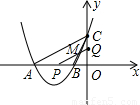
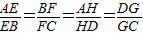 =k(k>0).阅读下段材料,回答下列问题:
=k(k>0).阅读下段材料,回答下列问题: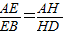 ,∴EH∥BD,∵
,∴EH∥BD,∵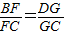 ,∴FG∥BD,∴FG∥EH.
,∴FG∥BD,∴FG∥EH.