Question

（1999•黄冈）已知抛物线y=x²+3mx+18m²-m与x轴交于A（x₁，0）、B（x₂，0）（x₁＜x₂）两点，与y轴交于点C（0，b），O为原点．
（1）求m的取值范围；
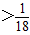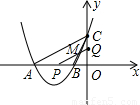
（2）若m，且OA+OB=3OC，求抛物线解析式及A，B，C的坐标；
（3）在（2）情形下，点P、Q分别从A、O两点同时出发（如图）以相同的速度沿AB、OC向B、C运动，连接PQ与BC交于M，设AP=k，问是否存在k值，使以P、B、M为顶点的三角形与△ABC相似？若存在，求所有k值；若不存在，请说明理由．

Answer 1

【答案】分析：（1）由于抛物线y=x²+3mx+18m²-m与x轴交于A（x₁，0）、B（x₂，0）（x₁＜x₂）两点，则判别式△＞0，解此不等式即可求出m的取值范围；
（2）由抛物线与一元二次方程的关系以及OA+OB=3OC，可求出m的值，进而求出抛物线的解析式及A，B，C的坐标；
（3）根据题意，当以P、B、M为顶点的三角形与△ABC相似时，由于点B与点B对应，则分两种情况．①P与A对应，②P与C对应．对于前一种情形，得到PQ∥AC，运用平行线分线段成比例定理可求出k值；对于后一种情形，得到△ABC∽△MBP，运用三角函数的定义及相似三角形的对应边成比例可求出k值．
解答：解：（1）依题意有△=（3m）²-4×（18m²-m）=m＞0，
∴m＞0；（3分）

（2）∵m，∴x₁＜0，x₂＜0，
由OA+OB=3•OC，有-x₁-x₂=3（18m²-m），
24m=3（18m²-m），
∴m=0（舍去）或m=．
∴y=x²+．（6分）
∴A（-8，0），B（-4，0），C（0，4）；（7分）

（3）当PQ∥AC时，△ABC∽△PBM，
则即，
∴（9分）
当PQ不与AC平行，
∠CAB=∠PMB时，△ABC∽△MBP．
过B作AC的垂线，D为垂足．
sinA=∴（10分）
∵∠ACB=∠MPB，∴Rt△CDB∽Rt△POQ．（11分）
∴∴
即
显然0＜k＜4．
∴=，∴
∴k=2．
∴存在k符合题目条件，即当k=或2时，
所得三角形与△ABC相似．（13分）
点评：本题主要考查了二次函数与一元二次方程的关系，三角函数的定义，相似三角形的性质等知识，综合性较强，难度较大．（3）题中，要根据相似三角形对应边和对应角的不同分类讨论，不要漏解．