题目内容
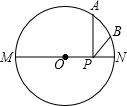已知：如图，A点是半圆上一个三等分点，B点是 | AN |
分析：通过作辅助线，根据“两点之间线段最短”可将AP+BP的最小值转化为求直角三角形的斜边长．
解答：
解：作A关于MN的对称点A′，根据圆的对称性，则A′必在圆上，
连接BA′交MN于P，连接PA，则PA+PB最小，此时PA+PB=PA′+PB=A′B，
连接OA、OA′、OB，
∵
=
，
∴∠AON=∠A′ON=60°．
∵
=
，
∴∠BON=
∠AON=30°．
∴∠A′OB=90°．
∴A′B=
=
=
．
即AP+BP的最小值是
．
解：作A关于MN的对称点A′，根据圆的对称性，则A′必在圆上，连接BA′交MN于P，连接PA，则PA+PB最小，此时PA+PB=PA′+PB=A′B，
连接OA、OA′、OB，
∵
|
| AN |
| 1 |
| 3 |
|
| MN |
∴∠AON=∠A′ON=60°．
∵
|
| AB |
|
| BN |
∴∠BON=
| 1 |
| 2 |
∴∠A′OB=90°．
∴A′B=
| OA′2+OB2 |
| 12+12 |
| 2 |
即AP+BP的最小值是
| 2 |
点评：本题主要考查圆心角，弧，弦之间的关系．
练习册系列答案
相关题目
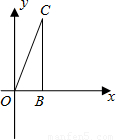
（2012•鄂州）已知，如图，△OBC中是直角三角形，OB与x轴正半轴重合，∠OBC=90°，且OB=1，BC=
OAM关于x轴对称，其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点，以点B为顶点且过点D的抛物线l交⊙P与另一点E．
OAM关于x轴对称，其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点，以点B为顶点且过点D的抛物线l交⊙P与另一点E．
已知，如图，△OBC中是直角三角形，OB与x轴正半轴重合，∠OBC=90°，且OB=1，BC=
，将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB1=OC，得到△OB1C1，将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB2=OC1，得到△OB2C2，…，如此继续下去，得到△OB2012C2012，则m=________．点C2012的坐标是________．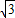
，将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB1=OC，得到△OB1C1，将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的m倍，使OB2=OC1，得到△OB2C2，…，如此继续下去，得到△OB2012C2012，则m= ．点C2012的坐标是 ．