Question

9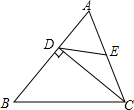．如图，△ABC中，CD⊥AB于D，E是AC的中点，若AD=6，CD=8，则DE的长等于5．

Answer 1

分析 利用勾股定理列式求出AC，再根据直角三角形斜边上的中线等于斜边的一半解答．

解答 解：∵CD⊥AB，AD=6，CD=8，
∴AC=$\sqrt{A{D}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10，
∵E是AC的中点，
∴DE=$\frac{1}{2}$AC=$\frac{1}{2}$×10=5．
故答案为：5．

点评 本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理，熟记性质是解题的关键．