题目内容

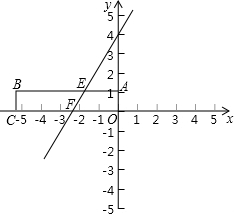
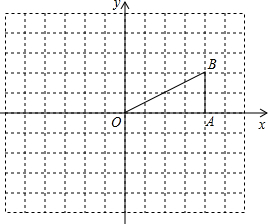
如图，在Rt△OAB中，∠OAB=90°，且点B的坐标为（4，2）．
（1）画出△OAB关于点O成中心对称的△OA1B1，并写出点B1的坐标；
（2）求出以点B1为顶点，并经过点B的二次函数关系式．
（1）∵∠OAB=90°，且点B的坐标为（4，2）．
∴A（4，0），
∴A、B关于O点的对称点的坐标为：A1（-4，0），B1（-4，-2）．
∴在平面直角坐标系中描出A1、B1点的坐标，再顺次连接就形成了△OA1B1．

（2）∵B1点是抛物线的顶点，其坐标为：（-4，-2），设抛物线的解析式为：y=a（x+4）2-2，且过B（4，2），
∴2=64a-2，
∴a=
1
16
，
抛物线的解析式为：y=
1
16
（x+4）2-2．
练习册系列答案
相关题目
已知如图，过O且半径为5的⊙P交x的正半轴于点M（2m，0）、交y轴的负半轴于点D，弧OBM与弧OAM关于x轴对称，其中A、B、C是过点P且垂直于x轴的直线与两弧及圆的交点．
（1）当m=4时，
①填空：B的坐标为______，C的坐标为______，D的坐标为______；
②若以B为顶点且过D的抛物线交⊙P于点E，求此抛物线的函数关系式和写出点E的坐标；
③除D点外，直线AD与②中的抛物线有无其它公共点并说明理由．
（2）是否存在实数m，使得以B、C、D、E为顶点的四边形组成菱形？若存在，求m的值；若不存在，请说明理由．
已知抛物线y=ax2上的点D、C与x轴上的点A（-6，0）、B（4，0）构成平行四边形ABCD，CD与y轴交于点E（0，6），求a的值及直线BC．
已知二次函数y=x2-mx+m-2．
（1）求证：无论m为任何实数，该二次函数的图象与x轴都有两个交点；
（2）当该二次函数的图象经过点（3，6）时，求二次函数的解析式；
（3）将直线y=x向下平移2个单位长度后与（2）中的抛物线交于A、B两点（点A在点B的左边），一个动点P自A点出发，先到达抛物线的对称轴上的某点E，再到达x轴上的某点F，最后运动到点B．求使点P运动的总路径最短的点E、点F的坐标，并求出这个最短总路径的长．
如图，在平面直角坐标系中放置一矩形ABCO，其顶点为A（0，1）、B（-3
3
，1）、C（-3
3
，0）、O（0，0）．将此矩形沿着过E（-
3
，1）、F（-
4
3
3
，0）的直线EF向右下方翻折，B、C的对应点分别为B′、C′．
（1）求折痕所在直线EF的解析式；
（2）一抛物线经过B、E、B′三点，求此二次函数解析式；
（3）能否在直线EF上求一点P，使得△PBC周长最小？如能，求出点P的坐标；若不能，说明理由．
如图，在平面直角坐标系xOy中，将抛物线C1：y=x2+3先向右平移1个单位，再向下平移7个单位得到抛物线C2．C2的图象与x轴交于A、B两点（点A在点B的左侧）．
（1）求抛物线C2的解析式；
（2）若抛物线C2的对称轴与x轴交于点C，与抛物线C2交于点D，与抛物线C1交于点E，连结AD、DB、BE、EA，请证明四边形ADBE是菱形，并计算它的面积；
（3）若点F为对称轴DE上任意一点，在抛物线C2上是否存在这样的点G，使以O、B、F、G四点为顶点的四边形是平行四边形？如果存在，请求出点G的坐标；如果不存在，请说明理由．
已知抛物线y=-
1
2
x2+bx+4上有不同的两点E（k+3，-k2+1）和F（-k-1，-k2+1）．
（1）求抛物线的解析式；
（2）如图，抛物线y=-
1
2
x2+bx+4与x轴和y轴的正半轴分别交于点A和B，M为AB的中点，∠PMQ在AB的同侧以M为中心旋转，且∠PMQ=45°，MP交y轴于点C，MQ交x轴于点D．设AD的长为m（m＞0），BC的长为n，求n和m之间的函数关系式；
（3）当m，n为何值时，∠PMQ的边过点F？
如图，已知抛物线y=-x2+mx+3与x轴的一个交点A（3，0）．
（1）你一定能分别求出这条抛物线与x轴的另一个交点B及与y轴的交点C的坐标，试试看；
（2）设抛物线的顶点为D，请在图中画出抛物线的草图．若点E（-2，n）在直线BC上，试判断E点是否在经过D点的反比例函数的图象上，把你的判断过程写出来；
（3）请设法求出tan∠DAC的值．
如图①，四边形ABCD是边长为5的正方形，以BC的中点O为原点，BC所在直线为x轴建立平面直角坐标系．抛物线y=ax2经过A、O、D三点，图②和图③是把一些这样的小正方形及其内部抛物线部分经过拼组得到的．

（1）a的值为______；
（2）图②中矩形EFGH的面积为______；
（3）图③中正方形PQRS的面积为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网