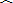��Ŀ����
��֪������y=-
x2+bx+4���в�ͬ������E��k+3��-k2+1����F��-k-1��-k2+1����
��1���������ߵĽ���ʽ��
��2����ͼ��������y=-
x2+bx+4��x���y���������ֱ��ڵ�A��B��MΪAB���е㣬��PMQ��AB��ͬ����MΪ������ת���ҡ�PMQ=45�㣬MP��y���ڵ�C��MQ��x���ڵ�D����AD�ij�Ϊm��m��0����BC�ij�Ϊn����n��m֮��ĺ�����ϵʽ��
��3����m��nΪ��ֵʱ����PMQ�ı߹���F��
| 1 |
| 2 |
��1���������ߵĽ���ʽ��
��2����ͼ��������y=-
| 1 |
| 2 |
��3����m��nΪ��ֵʱ����PMQ�ı߹���F��

��1��������y=-
x2+bx+4�ĶԳ���Ϊx=-
=b����1�֣�
���������ϲ�ͬ������E��k+3��-k2+1����F��-k-1��-k2+1������������ͬ��
���E�͵�F���������߶Գ���Գƣ���b=
=1����k��-2��
�������ߵĽ���ʽΪy=-
x2+x+4����2�֣�
��2��������y=-
x2+x+4��x��Ľ���ΪA��4��0������y��Ľ���ΪB��0��4����
��AB=4
��AM=BM=2
����3�֣�
�ڡ�PMQ�Ƶ�M��ABͬ����ת�����У���MBC=��DAM=��PMQ=45�㣬
�ڡ�BCM�У���BMC+��BCM+��MBC=180�㣬����BMC+��BCM=135�㣬
��ֱ��AB�ϣ���BMC+��PMQ+��AMD=180�㣬����BMC+��AMD=135�㣻
���BCM=��AMD��
���BCM����AMD����4�֣�
��
=
����
=
��n=
��
��n��m֮��ĺ�����ϵʽΪn=
��m��0������5�֣�
��3����F��-k-1��-k2+1����y=-
x2+x+4�ϣ�
�ཫF���뺯������ʽ�ã�-
(-k-1)2+(-k-1)+4=-k2+1��
����ã�k2-4k+3=0����k1=1��k2=3��
��F1��-2��0����F2��-4��-8������6�֣�
��MF��M��2��2����F1��-2��0������MFΪy=kx+b��
��
�����
��
��ֱ��MF�Ľ���ʽΪy=
x+1��
ֱ��MF��x�ύ��Ϊ��-2��0������y�ύ��Ϊ��0��1����
��MP����F��-2��0������n1=4-1=3��m1=
��
��MQ����F��-2��0������m2=4-��-2��=6��n2=
����7�֣�
��MF��M��2��2����F2��-4��-8������MFΪy=kx+b��
��
�����
��
��ֱ��MF�Ľ���ʽΪy=
x-
��
ֱ��MF��x�ύ��Ϊ��
��0������y�ύ��Ϊ��0��-
����
��MP����F��-4��-8������n3=4-��-
��=
��m3=
��
��MQ����F��-4��-8������m4=4-
=
��n4=
����8�֣�
�ʵ�
��
��
��
ʱ����PMQ�ı߹���F��
| 1 |
| 2 |
| b | ||
2��(-
|
���������ϲ�ͬ������E��k+3��-k2+1����F��-k-1��-k2+1������������ͬ��
���E�͵�F���������߶Գ���Գƣ���b=
| (k+3)+(-k-1) |
| 2 |
�������ߵĽ���ʽΪy=-
| 1 |
| 2 |
��2��������y=-
| 1 |
| 2 |
��AB=4
| 2 |
| 2 |
�ڡ�PMQ�Ƶ�M��ABͬ����ת�����У���MBC=��DAM=��PMQ=45�㣬
�ڡ�BCM�У���BMC+��BCM+��MBC=180�㣬����BMC+��BCM=135�㣬
��ֱ��AB�ϣ���BMC+��PMQ+��AMD=180�㣬����BMC+��AMD=135�㣻
���BCM=��AMD��
���BCM����AMD����4�֣�
��
| BC |
| AM |
| BM |
| AD |
| n | ||
2
|
2
| ||
| m |
| 8 |
| m |
��n��m֮��ĺ�����ϵʽΪn=
| 8 |
| m |
��3����F��-k-1��-k2+1����y=-
| 1 |
| 2 |
�ཫF���뺯������ʽ�ã�-
| 1 |
| 2 |
����ã�k2-4k+3=0����k1=1��k2=3��
��F1��-2��0����F2��-4��-8������6�֣�
��MF��M��2��2����F1��-2��0������MFΪy=kx+b��
��
|
|
��ֱ��MF�Ľ���ʽΪy=
| 1 |
| 2 |
ֱ��MF��x�ύ��Ϊ��-2��0������y�ύ��Ϊ��0��1����
��MP����F��-2��0������n1=4-1=3��m1=
| 8 |
| 3 |
��MQ����F��-2��0������m2=4-��-2��=6��n2=
| 4 |
| 3 |
��MF��M��2��2����F2��-4��-8������MFΪy=kx+b��
��
|
|
��ֱ��MF�Ľ���ʽΪy=
| 5 |
| 3 |
| 4 |
| 3 |
ֱ��MF��x�ύ��Ϊ��
| 4 |
| 5 |
| 4 |
| 3 |
��MP����F��-4��-8������n3=4-��-
| 4 |
| 3 |
| 16 |
| 3 |
| 3 |
| 2 |
��MQ����F��-4��-8������m4=4-
| 4 |
| 5 |
| 16 |
| 5 |
| 5 |
| 2 |
�ʵ�
|
|
|
|

��ϰ��ϵ�д�
�����Ŀ

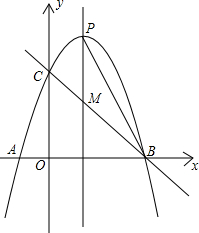
 ƽ���ı��Σ�������ڣ����R������ꣻ��������ڣ���˵�����ɣ�
ƽ���ı��Σ�������ڣ����R������ꣻ��������ڣ���˵�����ɣ�
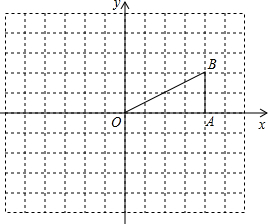
 ����C��0��-3����ֱ��y=-
����C��0��-3����ֱ��y=- OC�����ڵ�C����BOC=45�㣬BC��OC������ΪC��
OC�����ڵ�C����BOC=45�㣬BC��OC������ΪC��