题目内容
 如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.
如图,∠CAB=100°,∠ABF=110°,AC∥PD,BF∥PE,求∠DPE的度数.考点:平行线的性质
专题:
分析:先根据∠CAB=100°,AC∥PD得出∠BPD的度数,再由∠ABF=110°得出∠FBP的度数,根据∠DPE=∠BPD-∠FBP即可得出结论.
解答:解:∵∠CAB=100°,AC∥PD,
∴∠BPD=100°.
∵∠ABF=110°,BF∥PE,
∴∠FBP=180°-110°=70°,
∴∠DPE=∠BPD-∠FBP=100°-70°=30°.
∴∠BPD=100°.
∵∠ABF=110°,BF∥PE,
∴∠FBP=180°-110°=70°,
∴∠DPE=∠BPD-∠FBP=100°-70°=30°.
点评:本题考查的是平行线的性质,用到的知识点为:两直线平行,同位角相等,同旁内角互补.

练习册系列答案
相关题目
圆锥的母线长为5,底面半径为2,则此圆锥的侧面积是( )
| A、6π | B、8π |
| C、10π | D、20π |
下列从左到右的运算是因式分解的是( )
| A、2a2-2a+1=2a(a-1)+1 |
| B、(x-y)(x+y)=x2-y2 |
| C、9x2-6x+1=(3x-1)2 |
| D、x2+y2=(x-y)2+2xy |
关于x的一元二次方程方程x2-2x+k=0有两个不相等的实数解,则k的范围是( )
| A、k>0 | B、k>1 |
| C、k<1 | D、k≤1 |
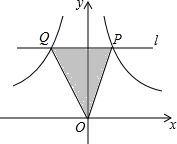 如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y=
如图,在平面直角坐标系中,直线l∥x轴,且直线l分别与反比例函数y= 如图,在平行四边形ABCD中,BE与CF分别平分∠ABC和∠BCD,交AD于E和两点,已知AD的长为8cm,EF的长为2cm,则AB的长为
如图,在平行四边形ABCD中,BE与CF分别平分∠ABC和∠BCD,交AD于E和两点,已知AD的长为8cm,EF的长为2cm,则AB的长为