题目内容
7．当x=2时，函数y=$\sqrt{（x-2）^{2}+4}$有最小值，是2．分析 由非负数的性质可知，（x-2）2+4≥4，当x=2时，最小值为4，由此进一步开方得出答案即可．
解答 解：∵（x-2）2+4≥4，当x=2时，最小值为4，
∴当x=2时，函数y=$\sqrt{（x-2）^{2}+4}$有最小值，是2．
故答案为：2，小，2．
点评 此题考查二次函数的最值，非负数的性质，利用非负数的性质得出（x-2）2+4的最小值是解决问题的关键．
练习册系列答案
相关题目
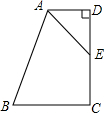如图．已知AD∥BC，DC⊥AD，∠BAD的平分线交CD于点E，且点E是CD的中点．问：