Question

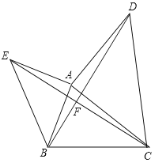
【题目】教材呈现：如图是华师版九年级上册数学教材第78页的部分内容．

例2 如图，在中，分别是边的中点，相交于点，求证：，

证明：连结．

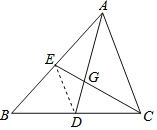
请根据教材提示，结合图①，写出完整的证明过程．

结论应用：在中，对角线交于点，为边的中点，、交于点．

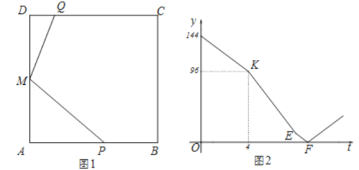
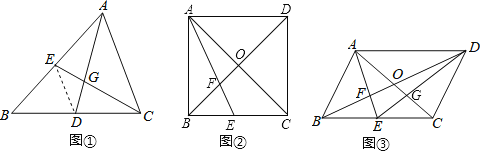
（1）如图②，若为正方形，且，则的长为　 　．

（2）如图③，连结交于点，若四边形的面积为，则的面积为　 　．

Answer 1

【答案】教材呈现：详见解析；结论应用：（1）；（2）6．

【解析】

教材呈现：如图①，连结．根据三角形中位线定理可得，，那么，由相似三角形对应边成比例以及比例的性质即可证明；

结论应用：（1）如图②．先证明，得出，那么，又，可得，由正方形的性质求出，即可求出；

（2）如图③，连接．由（1）易证．根据同高的两个三角形面积之比等于底边之比得出与的面积比，同理，与的面积比＝2，那么的面积的面积＝2（的面积的面积）＝，所以的面积，进而求出的面积．

教材呈现：

证明：

如图①，连结．

∵在中，分别是边的中点，

∴，

∴，

∴，

∴，

∴；

结论应用：

（1）解：如图②．

∵四边形为正方形，为边的中点，对角线、交于点，

∴，

∴，

∴，

∴，

∴，

∵，

∴，

∵正方形中，，

∴，

∴．

故答案为；

（2）解：如图③，连接．

由（1）知，，

∴．

∵与的高相同，

∴与的面积比，

同理，与的面积比＝2，

∴的面积的面积＝2（的面积的面积），

∴的面积，

∴的面积．

故答案为6．