题目内容
 已知,如图,AB和AC是夹角为127°的两面水泥墙俯视图,其中AB墙长为5米,AC墙长为15米,现借用这两面墙,并用16米长的篱笆(图中线段DE,EF的长度和)作另两面墙,围成一个四边形菜园ADEF,使得DE∥AC,DE⊥EF.设EF的长为x米,菜园ADEF的面积为y平方米.
已知,如图,AB和AC是夹角为127°的两面水泥墙俯视图,其中AB墙长为5米,AC墙长为15米,现借用这两面墙,并用16米长的篱笆(图中线段DE,EF的长度和)作另两面墙,围成一个四边形菜园ADEF,使得DE∥AC,DE⊥EF.设EF的长为x米,菜园ADEF的面积为y平方米.(1)用x分别表示AD,AF的长;
(2)求y关于x的函数关系式,并写出x的取值范围;
(3)当EF为何值时,菜园ADEF有最大值,最大值是多少?
(参考数据:sin53°≈0.8,cos53°≈0.6,tan37°≈0.75)
考点:解直角三角形的应用,二次函数的应用
专题:
分析:(1)如图,过点A作AM⊥DE于点M,构建矩形AMEF和直角△ADM,通过矩形的性质和解直角三角形进行解答即可;
(2)利用(1)中的数据和梯形的面积公式进行解答;
(3)利用(2)中的函数关系式进行求最值.
(2)利用(1)中的数据和梯形的面积公式进行解答;
(3)利用(2)中的函数关系式进行求最值.
解答: 解:(1)如图,过点A作AM⊥DE于点M,
解:(1)如图,过点A作AM⊥DE于点M,
∵DE∥AC,DE⊥EF,
∴四边形AMEF是矩形.
∴∠FAM=90°,EF=AM=x.
∵∠BAF=127°,
∴∠DAM=37°.
在直角△ADM中,DM=AM•tan37°≈0.75x,AD=
=
≈
x,
∴AF=16-x-0.75x=16-1.75x.
(2)y=
(AF+DE)•EF=
×(16-1.75x+16-x)x=
(32-2.75x)x=-
x2+16x.即y=-
x2+16x(0<x<
);
(3)由(2)知,y=-
x2+16x,
所以y=-
x2+16x=-
(x2-
)2+
.
所以 当x=
时,y最大=
.
 解:(1)如图,过点A作AM⊥DE于点M,
解:(1)如图,过点A作AM⊥DE于点M,∵DE∥AC,DE⊥EF,
∴四边形AMEF是矩形.
∴∠FAM=90°,EF=AM=x.
∵∠BAF=127°,
∴∠DAM=37°.
在直角△ADM中,DM=AM•tan37°≈0.75x,AD=
| AM |
| cos37° |
| AM |
| sin53° |
| 5 |
| 3 |
∴AF=16-x-0.75x=16-1.75x.
(2)y=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 11 |
| 8 |
| 11 |
| 8 |
| 64 |
| 7 |
(3)由(2)知,y=-
| 11 |
| 8 |
所以y=-
| 11 |
| 8 |
| 11 |
| 8 |
| 64 |
| 11 |
| 512 |
| 11 |
所以 当x=
| 64 |
| 7 |
| 512 |
| 11 |
点评:本题考查了解直角三角形的应用和二次函数的应用,求二次函数的最值时,也可以根据抛物线顶点坐标公式进行解答.

练习册系列答案
相关题目
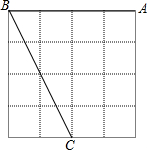 如图所示,每个小正方形的边长为1
如图所示,每个小正方形的边长为1 已知直线MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应点M1的坐标为
已知直线MN在直角坐标系中的位置如图所示,线段M1N1与MN关于y轴对称,则点M的对应点M1的坐标为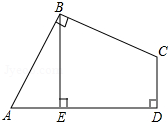 如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD,垂足为E.