题目内容
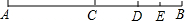 如图,AB=40,点C为AB的中点,点D为CB上的一点,点E为BD的中点,且EB=5,求CD的长.
如图,AB=40,点C为AB的中点,点D为CB上的一点,点E为BD的中点,且EB=5,求CD的长.
解:∵AB=40,点C为AB的中点,
∴CB= AB=
AB= ×40=20,
×40=20,
∵点E为BD的中点,且EB=5,
∴BD=2EB=10,
∴CD=CB-BD=20-10=10.
分析:点D为CB上一点,所以CD=BC-BD.只要求出BD的长即可,而BD=2BE,求出BE、BC,即可得出答案.
点评:本题考查了两点间的距离的应用,注意:求线段的长度,注意围绕线段的和、差、倍、分展开,若每一条线段长度均已确定,所求问题便迎刃而解.
∴CB=
 AB=
AB= ×40=20,
×40=20,∵点E为BD的中点,且EB=5,
∴BD=2EB=10,
∴CD=CB-BD=20-10=10.
分析:点D为CB上一点,所以CD=BC-BD.只要求出BD的长即可,而BD=2BE,求出BE、BC,即可得出答案.
点评:本题考查了两点间的距离的应用,注意:求线段的长度,注意围绕线段的和、差、倍、分展开,若每一条线段长度均已确定,所求问题便迎刃而解.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 (2013•通州区一模)如图,AB∥CD,点E在AB上,且DC=DE,∠AEC=70°,则∠D的度数是
(2013•通州区一模)如图,AB∥CD,点E在AB上,且DC=DE,∠AEC=70°,则∠D的度数是 如图,AB∥CD,点E在CD上,BC平分∠ABE,若∠C=20°,则∠ABE的度数是( )
如图,AB∥CD,点E在CD上,BC平分∠ABE,若∠C=20°,则∠ABE的度数是( ) 如图,AB=40,点C为AB的中点,点D为CB上的一点,点E为BD的中点,且EB=5,求CD的长.
如图,AB=40,点C为AB的中点,点D为CB上的一点,点E为BD的中点,且EB=5,求CD的长. 已知:如图,AB⊥CD于点O,∠BOE=40°,OF平分∠AOE,求∠FOC的度数.
已知:如图,AB⊥CD于点O,∠BOE=40°,OF平分∠AOE,求∠FOC的度数.