题目内容
 如图所示,在Rt△POQ中,∠POQ=90°,OP:OQ=3:2,点Q在反比例函数y=
如图所示,在Rt△POQ中,∠POQ=90°,OP:OQ=3:2,点Q在反比例函数y=| 4 |
| x |
| k |
| x |
分析:作QM⊥y轴,PN⊥y轴,分别与M,N两点,可以证得:∴△OQM∽△PON,根据相似三角形的性质即可证得ON•NP=9,根据反比例函数中k的几何意义即可求解.
解答: 解:作QM⊥y轴,PN⊥y轴,分别与M,N两点.
解:作QM⊥y轴,PN⊥y轴,分别与M,N两点.
∵∠MOQ=90°
∴∠QOx+∠POx=90°
又∵∠MOQ+∠NOP=90°,∠NOP+∠OPN=90°
∴∠MQO=∠NOP,∠QOM=∠ONP
∴△OQM∽△PON
∴
=
=
=
又∵MQ•OM=4
∴ON•NP=9
∴k=-9.
故答案是:-9.
 解:作QM⊥y轴,PN⊥y轴,分别与M,N两点.
解:作QM⊥y轴,PN⊥y轴,分别与M,N两点.∵∠MOQ=90°
∴∠QOx+∠POx=90°
又∵∠MOQ+∠NOP=90°,∠NOP+∠OPN=90°
∴∠MQO=∠NOP,∠QOM=∠ONP
∴△OQM∽△PON
∴
| OM |
| NP |
| MQ |
| ON |
| OQ |
| OP |
| 2 |
| 3 |
又∵MQ•OM=4
∴ON•NP=9
∴k=-9.
故答案是:-9.
点评:本题考查了反比例函数的性质,以及相似三角形的判定与性质,正确理解相似三角形的性质,理解反比例函数中k的意义是关键.

练习册系列答案
 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
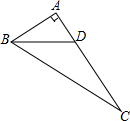 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( )
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=4,BD=5,则点D到BC的距离是( ) 21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB=
21、如图所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,∠A=55°,则∠DCB= 22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE.
22、如图所示,在Rt△ABC中,∠C=90°,∠A=30°.作AB的中垂线l分别交AB、AC及BC的延长线于点D、E、F,连接BE. 求证:EF=2DE. 如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB=
如图所示,在Rt△ABC中,∠C=90°,AC=6,sinB= 如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.
如图所示,在Rt△ABC中,AD平分∠BAC,交BC于D,CH⊥AB于H,交AD于F,DE⊥AB垂足为E,求证:四边形CFED是菱形.