题目内容
已知一次函数y=kx+b的图象经过点P(0,-3),且与函数y=
x+1的图象相交于点A(
,a).
(1)求a、k,b的值;
(2)若函数y=kx+b的图象与x轴的交点是B,函数y=
x+1的图象与y轴的交点是C,求四边形ABOC的面积(其中O为坐标原点).
| 1 |
| 2 |
| 8 |
| 3 |
(1)求a、k,b的值;
(2)若函数y=kx+b的图象与x轴的交点是B,函数y=
| 1 |
| 2 |
考点:两条直线相交或平行问题
专题:
分析:(1)运用待定系数法列出关于a、k,b的方程,即可解决问题.
(2)如图,作辅助线;求出B、C、N点的坐标;求出△AMN、△NOC的面积,即可解决问题.
(2)如图,作辅助线;求出B、C、N点的坐标;求出△AMN、△NOC的面积,即可解决问题.
解答: 解:(1)如图,∵函数y=
解:(1)如图,∵函数y=
x+1的图象过点A(
,a),
∴a=
×
+1=
;
由题意得:
,
解得:b=-3,k=2;
∴a、k,b的值分别为
、2、-3.
(2)如图,过点A作AM⊥x轴,
由题意得:AM=
;对于直线:y=
x+1,
当x-0时,y=1;当y=0时,x=-2,
∴OC=1,NO=2,MN=
+2=
.
∴S四边形ABOC=S△AMN-S△CON
=
×
×
-
×2×1
=
-1=
.
即四边形ABOC的面积为
.
 解:(1)如图,∵函数y=
解:(1)如图,∵函数y=| 1 |
| 2 |
| 8 |
| 3 |
∴a=
| 1 |
| 2 |
| 8 |
| 3 |
| 7 |
| 3 |
由题意得:
|
解得:b=-3,k=2;
∴a、k,b的值分别为
| 7 |
| 3 |
(2)如图,过点A作AM⊥x轴,
由题意得:AM=
| 7 |
| 3 |
| 1 |
| 2 |
当x-0时,y=1;当y=0时,x=-2,
∴OC=1,NO=2,MN=
| 8 |
| 3 |
| 14 |
| 3 |
∴S四边形ABOC=S△AMN-S△CON
=
| 1 |
| 2 |
| 14 |
| 3 |
| 7 |
| 3 |
| 1 |
| 2 |
=
| 49 |
| 9 |
| 40 |
| 9 |
即四边形ABOC的面积为
| 40 |
| 9 |
点评:该题主要考查了两条直线的相交或平行问题;解体的关键是数形结合,灵活运用方程或方程组等代数知识来分析、判断、推理或解答.对综合运用能力提出了一定的要求.

练习册系列答案
相关题目
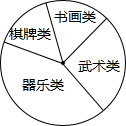 某校学生会准备调查八年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.
某校学生会准备调查八年级学生参加“武术类”、“书画类”、“棋牌类”、“器乐类”四类校本课程的人数.