题目内容
3.在平面直角坐标系中,△ACO为等腰直角三角形,AC=OC,C(-1,3).(1)如图1,求点A的坐标及OA的长;
(2)如图2,过C作CN⊥y轴于N,M为OA的中点,求MN的长.
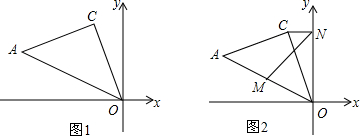
分析 (1)过C作BD∥x轴,过A作BD垂线交BD于点B,易证△ABC≌△COD,可得点A的坐标;
(2)根据题意可以求出点N,M坐标,即可求得MN的长度.
解答 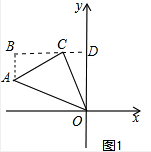 解:(1)如图1,过C作BD∥x轴,过A作BD垂线交BD于点B,
解:(1)如图1,过C作BD∥x轴,过A作BD垂线交BD于点B,
∵∠BCA+∠BAC=90°,∠DCO+∠BCA=90°,
∴∠BAC=∠DCO,
∵等腰直角△ACO中AC=CO.
在△ABC和△COD中,
$\left\{\begin{array}{l}{∠ABC=∠ODC=90°}\\{∠BAC=∠DCO}\\{AC=CO}\end{array}\right.$,
∴△ABC≌△COD,(AAS)
∴BC=OD,AB=CD,
∴点A的坐标为(-4,2),
∴OA=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$;
(2)∵点A的坐标为(-4,2),M为AO的中点,
∴M点坐标为(-2,1),
∵CN⊥y轴,
∴N点坐标为(0,3),
∴MN=$\sqrt{{2}^{2}+{2}^{2}}$=2$\sqrt{2}$.
点评 本题考查了全等三角形的判定和性质,勾股定理,等腰直角三角形的性质,平面直角坐标系中点与点的距离的计算,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
20. 如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
 如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )
如图所示是2004年3月份的日历表,任意圈出一竖列上相邻的三个数,这三个数的和不可能是( )| A. | 69 | B. | 54 | C. | 27 | D. | 40 |
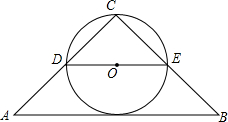 如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.
如图,在等腰Rt△ABC中,∠C=90°.点D,E分别为腰的中点,以DE长为直径作圆,圆心为O.请判断⊙O和底边AB是否相切,并说明理由.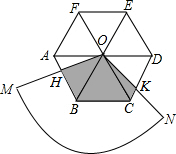 如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.
如图,圆心角为120°的扇形OMN,绕着正六边形ABCDEF的中心O旋转,OM交AB于H,ON交CD于K,OM>OA.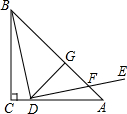 如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2$\sqrt{2}$,则△BDG的面积为96.
如图,等腰Rt△ABC中,∠C=90°,D为AC上一点,连接BD,将线段BD绕点D顺时针旋转90°得到线段DE,DE与AB相交于点F,过点D作DG⊥AB,垂足为点G.若EF=5,CD=2$\sqrt{2}$,则△BDG的面积为96.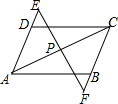 如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.
如图,AB=CD,AD=BC,P为AC上任一点,过P的直线分别交AD,CB的延长线于点E,F.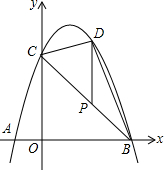 如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).
如图,抛物线y=-x2+bx+c经过点A,B,C,已知点A(-1,0),点C(0,3).