题目内容
1.观察下列各运算:($\sqrt{2}-1$)($\sqrt{2}+1$)=1,($\sqrt{3}-\sqrt{2}$)($\sqrt{3}+\sqrt{2}$)=1,…($\sqrt{2007}-\sqrt{2006}$)($\sqrt{2007}+\sqrt{2006}$)=1,
($\sqrt{2008}-\sqrt{2007}$)($\sqrt{2008}+\sqrt{2007}$)=1.利用上面的规律计算
$\frac{1}{1+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+…+\frac{1}{\sqrt{2006}+\sqrt{2007}}$$+\frac{1}{\sqrt{2007}+\sqrt{2008}}$.
分析 先分母有理化,求出以后合并同类二次根式,即可得出答案.
解答 解:原式=$\frac{1×(\sqrt{2}-1)}{(\sqrt{2}+1)×(\sqrt{2}-1)}$+$\frac{1×(\sqrt{3}-\sqrt{2})}{(\sqrt{3}+\sqrt{2})×(\sqrt{3}-\sqrt{2})}$+$\frac{1×(\sqrt{4}-\sqrt{3})}{(\sqrt{4}+\sqrt{3})×(\sqrt{4}-\sqrt{3})}$+…+$\frac{1×(\sqrt{2008}-\sqrt{2007})}{(\sqrt{2008}+\sqrt{2007})×(\sqrt{2008}-\sqrt{2007})}$
=$\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+$\sqrt{4}$-$\sqrt{3}$+…+$\sqrt{2008}$-$\sqrt{2007}$
=$\sqrt{2008}$-1.
点评 本题考查了二次根式的乘除法和分母有理化,能正确分母有理化是解此题的关键.

练习册系列答案
相关题目
13.若(x+a)(x-b)=x2+mx+n,则m,n的值分别是( )
| A. | m=a-b,n=ab | B. | m=-(a-b),n=ab | C. | m=a-b,n=-ab | D. | m=-(a-b),n=-ab |
10.一元二次方程x2+x+$\frac{1}{3}$=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
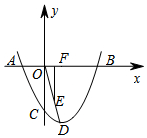 如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).
如图,一抛物线经过点A(-2,0),B(6,0),C(0,-3),D为抛物线的顶点,过OD的中点E,作EF⊥x轴于点F,G为x轴上一动点,M为抛物线上一动点,N为直线EF上一动点,当以F、G、M、N为顶点的四边形是正方形时,点G的坐标为(4-2$\sqrt{6}$,0)、(-4,0)、(4+2$\sqrt{6}$,0)或(4,0).