题目内容
20.如图,在平面直角坐标系中,AB=AC=10,线段BC在x轴上,BC=12,点B的坐标为(-3,0),线段AB交y轴于点E,过A作AD⊥BC于D,动点P从原点出发,以每秒3个单位的速度沿x轴向右运动,设运动的时间为t秒.(1)当△BPE是等腰三角形时,求t的值;
(2)若点P运动的同时,△ABC以B为位似中心向右放大,且点C向右运动的速度为每秒2个单位,△ABC放大的同时高AD也随之放大,当以EP为直径的圆与动线段AD所在直线相切时,求t的值和此时点C的坐标.
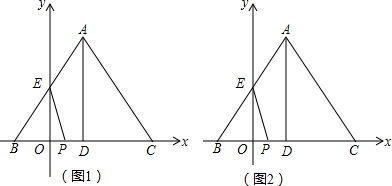
分析 (1)首先求出直线AB的解析式,进而分别利用①当BE=BP时,②当EB=EP时,③当PB=PE时,得出t的值即可;
(2)首先得出△PGF∽△POE,再利用在Rt△EOP中:EP2=OP2+EO2,进而求出t的值以及C点坐标.
解答 解:(1)∵AB=AC,AD⊥BC,
∴BD=CD=6,
∵AB=10,
∴AD=8,
∴A(3,8),
设直线AB的解析式为:y=kx+b,则$\left\{\begin{array}{l}{-3k+b=0}\\{3k+b=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=4}\end{array}\right.$,
∴直线AB的解析式为:y=$\frac{3}{4}$x+4,
∴E(0,4),
∴BE=5,
当△BPE是等腰三角形有三种情况:
①当BE=BP时,3+3t=5,解得:t=$\frac{2}{3}$;
②当EB=EP时,3t=3,解得:t=1;
③当PB=PE时,
∵PB=PE,AB=AC,∠ABC=∠PBE,
∴∠PEB=∠ACB=∠ABC,
∴△PBE∽△ABC,
∴$\frac{BP}{AB}$=$\frac{BE}{BC}$,
∴$\frac{3+3t}{10}$=$\frac{5}{12}$,解得:t=$\frac{7}{18}$,
综上:t=$\frac{2}{3}$或t=1或t=$\frac{7}{18}$;
(2)由题意得:C(9+2t,0),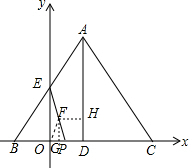
∴BC=12+2t,BD=CD=6+t,OD=3+t,
设F为EP的中点,连接OF,作FH⊥AD,FG⊥OP,
∵FG∥EO,
∴△PGF∽△POE,
∴PG=OG=$\frac{3}{2}$t,FG=$\frac{1}{2}$EO=2,∴F($\frac{3}{2}$t,2),
∴FH=GD=OD-OG=3+t-$\frac{3}{2}$t=3-$\frac{1}{2}$t,
∵⊙F与动线段AD所在直线相切,FH=$\frac{1}{2}$EP=3-$\frac{1}{2}$t,
在Rt△EOP中:EP2=OP2+EO2
∴4(3-$\frac{1}{2}$t)2=(3t)2+16
解得:t1=1,t2=-$\frac{5}{2}$(舍去),
∴当t=1时⊙F与动线段AD所在直线相切,此时C(11,0).
点评 此题主要考查了圆的综合以及相似三角形的判定与性质以及等腰三角形的性质等知识,利用分类讨论得出是解题关键.

 阅读快车系列答案
阅读快车系列答案| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
 如图,一个直角三角板的直角顶点落右直尺上,若∠1=56°,则∠2的度数为34°.
如图,一个直角三角板的直角顶点落右直尺上,若∠1=56°,则∠2的度数为34°.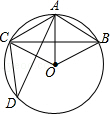 如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论:
如图,在半径为6cm的⊙O中,点A是劣弧$\widehat{BC}$的中点,点D是优弧$\widehat{BC}$上一点,且∠D=30°,下列四个结论: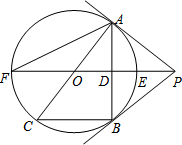 如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
 在平面直角坐标系中,已经A(8,0),B(0,6)
在平面直角坐标系中,已经A(8,0),B(0,6)