题目内容
4．
如图，有甲，乙两个可以自由转动的转盘，若同时转动，则停止后指针都落在阴影区域内的概率是$\frac{1}{2}$．
分析 根据几何概率的定义，分别求出两圆中阴影部分所占的面积，即可求出停止后指针都落在阴影区域内的概率．
解答 解：指针指向甲中阴影的概率是$\frac{3}{4}$，指针指向乙中阴影的概率是$\frac{2}{3}$，
停止后指针都落在阴影区域内的概率是$\frac{3}{4}$×$\frac{2}{3}$=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 此题考查学生对简单几何概型的掌握情况，既避免了单纯依靠公式机械计算的做法，又体现了数学知识在现实生活、甚至娱乐中的运用，体现了数学学科的基础性．两步完成的事件的概率=第一步事件的概率与第二步事件的概率的积．
练习册系列答案
导学全程练创优训练系列答案
相关题目
14．计算：（$\frac{21}{26}$）3×（$\frac{13}{14}$）4×（$\frac{4}{3}$）5=（ ）
| A． | $\frac{13}{33}$ | B． | $\frac{104}{63}$ | C． | $\frac{2×13}{3×7}$ | D． | $\frac{23×13}{32×7}$ |
15．在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只，某学习小组做摸球实验，将球搅匀后从中随机摸出一个球记下颜色，再把它放回袋中，不断重复．下表是活动进行中的一组统计数据：
（1）完成上表；
（2）“摸到白球”的概率的估计值是0.6 （精确到0.1）；
（3）试估算口袋中黑、白两种颜色的球各有多少只？
| 摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数m | 59 | 96 | 116 | 290 | 480 | 601 |
| 摸到白球的频率$\frac{m}{n}$ | 0.59 | 0.64 | 0.58 | 0.58 | 0.60 | 0.601 |
（2）“摸到白球”的概率的估计值是0.6 （精确到0.1）；
（3）试估算口袋中黑、白两种颜色的球各有多少只？
如图，点P在函数y=$\frac{\sqrt{3}}{x}$（x＞0）的图象上运动，O为坐标原点，点A为PO的中点，以点P为圆心，PA为半径作⊙P，则当⊙P与坐标轴相切时，点P的坐标为（$\sqrt{3}$，1）或（1，$\sqrt{3}$）．
如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，下列结论：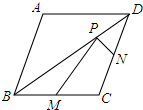
如图，已知菱形ABCD的两条对角线长分别是3和4，点M、N分别是边BC、CD的中点，点P是对角线上的一点，则PM+PN的最小值是$\frac{5}{2}$．
如图，方格中，每个小正方形的边长都是单位1，△ABC在平面直角坐标系中的位置如图．