题目内容
4.不改变分式的值,使分子、分母的最高次项的系数为正,则$\frac{-{a}^{3}+{a}^{2}-1}{1-{a}^{3}-{a}^{2}}$=$\frac{{a}^{3}-{a}^{2}+1}{{a}^{3}+{a}^{2}-1}$.分析 先将分子、分母均按同一字母的降幂排列,分子、分母第一项的系数为负,则添带负号的括号,注意分子、分母和分式本身的符号的改变.
解答 解:原式=$\frac{-{a}^{3}+{a}^{2}-1}{-{a}^{3}-{a}^{2}+1}$=$\frac{{a}^{3}-{a}^{2}+1}{{a}^{3}+{a}^{2}-1}$.
故答案为:$\frac{{a}^{3}-{a}^{2}+1}{{a}^{3}+{a}^{2}-1}$.
点评 本题考查的是分式的基本性质,解题的关键是正确运用分式的基本性质,分式的分子、分母及本身的符号,任意改变其中的两个,分式的值不变.

练习册系列答案
相关题目
14.下列四个几何体中,主视图与其它三个不同的是( )
| A. |  | B. |  | C. |  | D. |  |
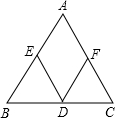 如图,在△ABC中,DE∥AC,DF∥AB.
如图,在△ABC中,DE∥AC,DF∥AB.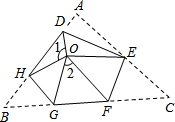 如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.
如图,将△ABC三个角分别沿DE、HG、EF翻折,三个顶点均落在点O处,则∠1+∠2的度数为180°.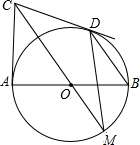 如图,AB为⊙O的直径,CA、CD分别切⊙O于A、D,CO的延长线交⊙O于M,连BD、DM.
如图,AB为⊙O的直径,CA、CD分别切⊙O于A、D,CO的延长线交⊙O于M,连BD、DM.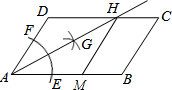 如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H;过点H作HM∥BC交AB于M.则下列结论:①AG平分∠DAB,②S△ADH=$\frac{1}{2}$S四边形ABCH,③△ADH是等腰三角形,④四边形ADHM为菱形.其中正确的是①③④.
如图,在平行四边形ABCD中,AB>AD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于$\frac{1}{2}$EF的长为半径画弧,两弧交于点G;作射线AG交CD于点H;过点H作HM∥BC交AB于M.则下列结论:①AG平分∠DAB,②S△ADH=$\frac{1}{2}$S四边形ABCH,③△ADH是等腰三角形,④四边形ADHM为菱形.其中正确的是①③④.