题目内容
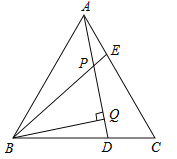
【题目】已知：如图，点P是正方形ABCD内一点，连接PA、PB、PC．
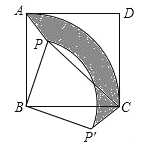
（1）将△PAB绕点B顺时针旋转90°得到△P'CB，若AB=m，PB=n（n＜m）．求△PAB旋转过程中边PA扫过区域（阴影部分）的面积；
（2）若PA=
，PB=
，∠APB=135°，求PC的长．
【答案】（1）
（m2﹣n2）；（2）
．
【解析】试题分析：（1）利用旋转性质，S△ABP=S△CBP′，求扇形面积.(2) 连接PP′,利用旋转，勾股定理求PC值.
试题解析：
解：（1）由旋转的性质可知，S△ABP=S△CBP′，
∴△PAB旋转过程中边PA扫过区域面积=
﹣
=
（m2﹣n2）；
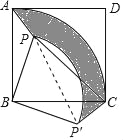
（2）连接PP′，
由旋转的性质可知，∠BP′C=∠APB=135°，∠PBP′=90°，BP′=BP=2
，P′C=PA=
，
∴PP′=
=4，∠PP′C=90°，
∴PC=
=3
．
练习册系列答案
相关题目
