题目内容
20.已知a1=x-1(x≠1且x≠2),a2=$\frac{1}{1-{a}_{1}}$,a3=$\frac{1}{1-{a}_{2}}$,…,an=$\frac{1}{1-{a}_{n-1}}$,则a2015等于( )| A. | $\frac{2-x}{1-x}$ | B. | x+1 | C. | x-1 | D. | $\frac{1}{2-x}$ |
分析 按照规定的运算方法,计算得出数值,进一步找出数字循环的规律,利用规律找出答案即可.
解答 解:∵a1=x-1,
a2=$\frac{1}{2-x}$,a3=$\frac{1}{1-{a}_{2}}$=$\frac{2-x}{1-x}$,a4=$\frac{1}{1{-a}_{3}}$=x-1,…
∴x-1,$\frac{1}{2-x}$,$\frac{2-x}{1-x}$循环出现,
∵2015÷3=671…2,
∴a2015的值与a2的值相同,
∴a2015=$\frac{1}{2-x}$,
故选D.
点评 此题考查数字的变化规律,找出数字之间的运算规律,利用规律解决问题是解答此题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
11.已知点P(m+3,m+1)在x轴上,则P点的坐标为( )
| A. | (0,2) | B. | (2,0) | C. | (4,0) | D. | (0,-4) |
9.甲市欲将一批水果运往乙市销售,现有火车、汽车两种运输方式,这两种运输方式的所需费用如下表(途中费用是指每公里所需的运输费用):
设甲、乙两市间的距离为xkm,
(1)如果用y1,y2分别表示使用火车、汽车运输时的总支出费用,分别写出y1,y2与x间的表达式;
(2)当x=300时,应采用哪种运输方式,才能使运输时的总支出费用最小?
| 运输工具 | 途中费用(元/km) | 装卸总费用(元) |
| 火车 | 4 | 2000 |
| 汽车 | 8 | 1000 |
(1)如果用y1,y2分别表示使用火车、汽车运输时的总支出费用,分别写出y1,y2与x间的表达式;
(2)当x=300时,应采用哪种运输方式,才能使运输时的总支出费用最小?
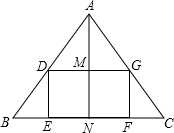 如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.
如图,在△ABC中,AB=AC=10,BC=12,矩形DEFG的顶点位于△ABC的边上,设EF=x,SDEFG=y.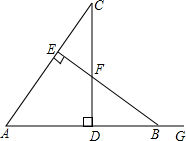 如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.
如图,CD⊥AB于点D,BE⊥AC于点E,△ABE≌△ACD,∠C=42°,AB=9,AD=6,G为AB延长线上一点.