Question

如图，以点G（4，0）为圆心，2为半径的圆与x轴交于A、B两点，已知抛物线y=-

1

6

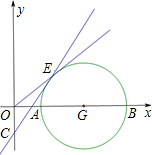x²+bx+c过点A和点B，与y轴交于点C．
（1）求抛物线的函数关系式；
（2）求出点C的坐标，并在图中画出此抛物线的大致图象；
（3）点F（8，m）在抛物线y=-

1

6

x²+bx+c上，点P为此抛物线对称轴上一个动点，求PF+PB的最小值；
（4）OE是⊙G的切线，点E是切点，在抛物线上是否存在一点Q，使△COQ的面积等于△COE的面积？若存在，求出点Q的坐标；若不存在，请说明理由．

Answer 1

分析：（1）根据以点G（4，0）为圆心，2为半径的圆与x轴交于A、B两点，求得点A的坐标为（2，0），点B的坐标为（6，0），然后代入抛物线y=-

1

6

x²+bx+c求得函数的解析式即可；
（2）首先求得抛物线与y轴的交点点C的坐标，然后将y=-

1

6

x²+

4

3

x-2配方成y=

1

6

（x-4）²+

2

3

的形式，从而求得顶点坐标，即可作出函数的图象；
（3）根据F（8，m）在抛物线y=-

1

6

x²+

4

3

x-2上，求得点F的坐标，连接AF，则与抛物线的对称轴的交点为点P，此时PF+PB的最小，然后利用勾股定理求得AF的长即为最小值；
（4）连接EG，根据OE是⊙G的切线，得到∠OEG=90°，然后利用勾股定理求得OE的长即可，进而得出E点坐标，求出即可．

解答：解：（1）∵以点G（4，0）为圆心，2为半径的圆与x轴交于A、B两点，
点A的坐标为（2，0），点B的坐标为（6，0），
∵抛物线y=-

1

6

x²+bx+c过点A和点B，
∴

- 1 6 ×22+2b+c=0 - 1 6 ×62+6b+c=0

，
解得：

b= 4 3 c=-2

，
∴此抛物线的函数关系式为：y=-

1

6

x²+

4

3

x-2；

（2）∵C点为抛物线与y轴的交点，
∴当x=0时，y=-2，
∴点C的坐标为（0，-2）；
∵y=-

1

6

x²+

4

3

x-2=-

1

6

（x²-8x）-2=-

1

6

（x-4）²+

2

3

，
∴此抛物线的顶点坐标为（4，

2

3

），如图：

（3）∵点F（8，m）在抛物线y=-

1

6

x²+

4

3

x-2上，
∴点F的坐标为（8，-2），
连接AF，则与抛物线的对称轴的交点为点P，此时PF+PB的最小，
∴PA=PB，
∴PF+PB=PA+PF=AF=

(8-2)2+22

=2

10

；
∴PF+PB的最小值为2

10

；

（4）连接EG，作ER⊥OB，ET⊥y轴，
∴EG=2，
∵OE是⊙G的切线，
∴∠OEG=90°，
∴OE=2

3

．
∵EG=2，OG=4，
∴∠EOG=30°，
∴∠EGO=90°-∠EOG=90°-30°=60°，
∴RG=1，
∴ER=

3

，OR=3，
∴ET=3，
∴△COE的面积为：

1

2

×2×3=3，
∴△COQ的面积为3，
当Q点横坐标为3时，
y=-

1

6

x²+

4

3

x-2=

1

2

；
∴Q点的坐标为：（3，

1

2

），
当Q点横坐标为-3时，
y=-

1

6

x²+

4

3

x-2；
y=-

15

2

，
∴Q点的坐标为：（-3，-

15

2

），
∴点Q的坐标为：（-3，-

15

2

），（3，

1

2

）．

点评：本题考查了二次函数的综合知识，特别是题目中与几何知识结合起来，更是中考中的常见考题．