题目内容
【题目】如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段O M0绕原点O沿逆时针方向旋转45°,再将其延长到M1,使得M1 M0⊥O M0,得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2,使得M2M1⊥OM1,得到线段OM2,如此下去,得到线段OM3,OM4,…,OMn
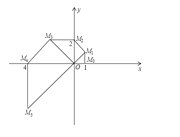
(1)写出点M5的坐标;
(2)求△M5OM6的周长;
(3)我们规定:把点Mn(xn,yn)(n=0,1,2,3…)的横坐标xn,纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Mn的“绝对坐标”.根据图中点Mn的分布规律,请你猜想点Mn的“绝对坐标”,并写出来.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当点M在x轴上时,点
;(3)当点M在x轴上时,点![]() 的“绝对坐标”为
的“绝对坐标”为![]() ;当点M在y轴上时,点
;当点M在y轴上时,点![]() 的“绝对坐标”为
的“绝对坐标”为![]() ;当点M在各象限的角平分线上时,点
;当点M在各象限的角平分线上时,点![]() 的“绝对坐标”为
的“绝对坐标”为![]()
【解析】
(1)根据等腰直角三角形的性质分别求出M1、M2、M3、M4的坐标,然后求M5的坐标.
(2)要求周长,就先根据各点的坐标求出三角形的三边长,然后再求周长.
(3)点Mn的“绝对坐标”可分三类情况来一一当点M在x轴上时;当点M在各象限的分角线上时;当点M在y轴上时.
(1)由题得:OM0=M0M1,
∴M1的坐标为(1,1).
同理M2的坐标为(0,2),
M3的坐标为(-2,2),
M4的坐标为(-4,0),
M5(-4,-4);
(2)由规律可知,OM5=![]() ,
,
M5M6=![]() ,OM6=8,
,OM6=8,
∴△ M5OM6的周长为8+![]() ;
;
(3)由题意知,OM0旋转8次之后回到x轴的正半轴,
在这8次旋转中,点分别落在坐标象限的分角线上或x轴或y轴上,
但各点“绝对坐标”的横、纵坐标均为非负数,
因此,各点的“绝对坐标”可分三种情况:
①当n=4k时(其中k=0,1,2,3,),点在x轴上,则Mn![]() ;
;
②当n=4k-2时(其中k=1,2,3,),点在y轴上,点Mn![]() ;
;
③当n=2k-1时,点在各象限的角平分线上,则点Mn![]()

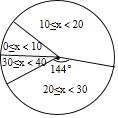
【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.