题目内容
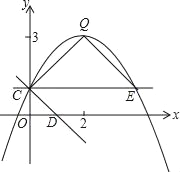
【题目】如图,直线y=k1x+b与双曲线![]() 相交于A(1,2),B(m,-1)两点.
相交于A(1,2),B(m,-1)两点.

(1)求直线和双曲线的表达式;
(2)求直线AB与x轴的交点C的坐标及ΔAOB的面积;
(3)观察图像,请直接写出使不等式k1x+b>![]() 成立的x的取值范围.
成立的x的取值范围.
【答案】(1)双曲线的解析式为y=![]() ;直线的解析式为:y=x+1.(2)1.5;(3)x>1或-2<x<0.
;直线的解析式为:y=x+1.(2)1.5;(3)x>1或-2<x<0.
【解析】
(1)先把A点坐标代入![]() 求出k2=2,得到双曲线的解析式为y=
求出k2=2,得到双曲线的解析式为y=![]() ,再把B(m,-1)代入y=
,再把B(m,-1)代入y=![]() 确定B点坐标,然后利用待定系数法确定一次函数的解析式;
确定B点坐标,然后利用待定系数法确定一次函数的解析式;
(2)在直线解析式中令y=0,可求出x的值,从而求出点C的坐标,再根据三角形面积公式求出ΔAOB的面积即可;
(3)观察函数图象得到当x>1或-2<x<0时,一次函数图象都在反比例函数图象上方,即k1x+b>![]() .
.
(1)∵双曲线![]() 经过点A(1,2),
经过点A(1,2),
∴k2=2,
∴双曲线的解析式为y=![]() ;
;
∵点B(m,-1)在双曲线y=![]() 上,
上,
∴m=-2,
∴B点坐标为(-2,-1),
把点A(1,2),B(-2,-1)代入y=k1x+b 得,
 ,解得
,解得![]() ,
,
∴直线的解析式为:y=x+1.
(2)在y=x+1中,令y=0,则x=-1,
∴C(-1,0)
∴S△AOB=![]() =1.5.
=1.5.
(3)由图可知x>1或-2<x<0.

 阅读快车系列答案
阅读快车系列答案【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
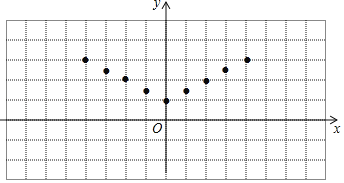
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
【题目】在一个不透明的口袋里装有仅颜色不同的黑、白两种颜色的球20只,某学习小组做摸球实验.将球搅匀后从中随机摸出一个球,记下颜色,再把它放回袋中,不断重复,下表是活动进行中记下的一组数据
摸球的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数 | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
(1)请你估计,当n很大时,摸到白球的频率将会接近 (精确到0.1).
(2)假如你去摸一次,你摸到白球的概率是 ,摸到黑球的概率是 .
(3)试估算口袋中黑、白两种颜色的球有多少只.