题目内容
 如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为
如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为考点:切线的性质,切割线定理,相似三角形的性质
专题:压轴题
分析:连接OE、OF,由切线的性质结合结合直角三角形可得到正方形OECF,并且可求出⊙O的半径为0.5a,则BF=a-0.5a=0.5a,再由切割线定理可得BF2=BH•BG,利用方程即可求出BH,然后又因OE∥DB,OE=OH,利用相似三角形的性质即可求出BH=BD,最终由CD=BC+BD,即可求出答案.
解答: 解:如图,连接OE、OF,
解:如图,连接OE、OF,
∵由切线的性质可得OE=OF=⊙O的半径,∠OEC=∠OFC=∠C=90°,
∴OECF是正方形,
∵由△ABC的面积可知
×AC×BC=
×AC×OE+
×BC×OF,
∴OE=OF=
a=EC=CF,BF=BC-CF=0.5a,GH=2OE=a,
∵由切割线定理可得BF2=BH•BG,
∴
a2=BH(BH+a),
∴BH=
a或BH=
a(舍去),
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴
=
,
∴BH=BD,CD=BC+BD=a+
a=
a.
故答案为:
a.
 解:如图,连接OE、OF,
解:如图,连接OE、OF,∵由切线的性质可得OE=OF=⊙O的半径,∠OEC=∠OFC=∠C=90°,
∴OECF是正方形,
∵由△ABC的面积可知
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴OE=OF=
| 1 |
| 2 |
∵由切割线定理可得BF2=BH•BG,
∴
| 1 |
| 4 |
∴BH=
-1+
| ||
| 2 |
-1-
| ||
| 2 |
∵OE∥DB,OE=OH,
∴△OEH∽△BDH,
∴
| OE |
| OH |
| BD |
| BH |
∴BH=BD,CD=BC+BD=a+
-1+
| ||
| 2 |
1+
| ||
| 2 |
故答案为:
1+
| ||
| 2 |
点评:考查了切线的性质,本题需仔细分析题意,结合图形,利用相似三角形的性质及切线的性质即可解决问题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

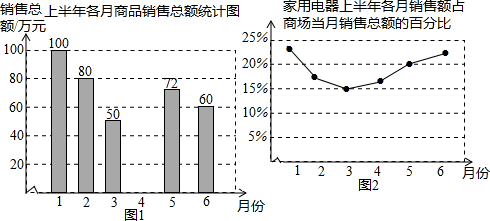
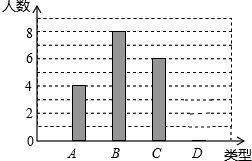 某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题: 为了了解八年级800名学生寒假的读书情况,数学小组随机调查了50名八年级学生,并将统计数据制成了扇形统计图如图,其中读1册的有13人,则该校八年级学生中读书册数为3册的约有
为了了解八年级800名学生寒假的读书情况,数学小组随机调查了50名八年级学生,并将统计数据制成了扇形统计图如图,其中读1册的有13人,则该校八年级学生中读书册数为3册的约有