题目内容
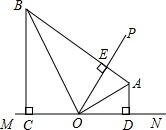 如图,点A,B分别是∠NOP,∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则以下结论错误的是( )
如图,点A,B分别是∠NOP,∠MOP平分线上的点,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,则以下结论错误的是( )| A、AD+BC=AB |
| B、∠AOB=90° |
| C、与∠CBO互余的角有2个 |
| D、点O是CD的中点 |
考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得AD=AE,BC=BE,再利用“HL”证明Rt△AOD和Rt△AOE全等,根据全等三角形对应边相等可得OD=OE,∠AOE=∠AOD,同理可得OC=OE,∠BOC=∠BOE,然后求出∠AOB=90°,然后对各选项分析判断即可得解.
解答:解:∵点A,B分别是∠NOP,∠MOP平分线上的点,
∴AD=AE,BC=BE,
∵AB=AE+BE,
∴AB=AD+BC,故A选项结论正确;
在Rt△AOD和Rt△AOE中,
,
∴Rt△AOD≌Rt△AOE(HL),
∴OD=OE,∠AOE=∠AOD,
同理可得OC=OE,∠BOC=∠BOE,
∴∠AOB=
×180°=90°,故B选项结论正确;
与∠CBO互余的角有∠COB,∠EOB,∠OAD,∠OAE共4个,故C选项结论错误;
∵OC=OD=OE,
∴点O是CD的中点,故D选项结论正确.
故选C.
∴AD=AE,BC=BE,
∵AB=AE+BE,
∴AB=AD+BC,故A选项结论正确;
在Rt△AOD和Rt△AOE中,
|
∴Rt△AOD≌Rt△AOE(HL),
∴OD=OE,∠AOE=∠AOD,
同理可得OC=OE,∠BOC=∠BOE,
∴∠AOB=
| 1 |
| 2 |
与∠CBO互余的角有∠COB,∠EOB,∠OAD,∠OAE共4个,故C选项结论错误;
∵OC=OD=OE,
∴点O是CD的中点,故D选项结论正确.
故选C.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,余角的定义,熟记各性质并准确识图是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△ABC中,AB=AC,DE是AB边的垂直平分线,分别交AB、AC于D、E,△BEC的周长是14cm,BC=5cm,则AB的长是( )
如图,在△ABC中,AB=AC,DE是AB边的垂直平分线,分别交AB、AC于D、E,△BEC的周长是14cm,BC=5cm,则AB的长是( )| A、14cm | B、9cm |
| C、19cm | D、12cm |
任取一条线段,使它能够盖住数轴上的至少1999个整数点,则这条线段长度l需满足的条件是( )
| A、l=1999 |
| B、l≥1998 |
| C、l≥1999 |
| D、l≥2000 |
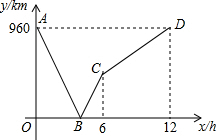 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答:当出发几个小时后,两车相距为240km?( )
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答:当出发几个小时后,两车相距为240km?( )| A、3或6 | B、3 | C、3或5 | D、5 |
下列说法中,正确的是( )
| A、正整数、负整数统称为整数 |
| B、正分数和负分数统称为分数 |
| C、0既是正整数又是负整数 |
| D、正数和负数统称为有理数 |
 如图一共有
如图一共有 如图,在平行四边形ABCD中,E是BC中点,AF⊥CD于点F,AE=4,AF=6,则△AEF的面积是
如图,在平行四边形ABCD中,E是BC中点,AF⊥CD于点F,AE=4,AF=6,则△AEF的面积是 画出如图主视图、俯视图、左视图.
画出如图主视图、俯视图、左视图.