题目内容
 (1)如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=2.2cm,AC=3.7cm,则点D到AB边的距离是
(1)如图,在Rt△ABC中,∠C=90°,BD是三角形的角平分线,交AC于点D,AD=2.2cm,AC=3.7cm,则点D到AB边的距离是(2)在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为50°,则∠B的度数为
考点:角平分线的性质,等腰三角形的性质
专题:
分析:(1)先根据AD=2.2cm,AC=3.7cm求出CD的长,再由角平分线的性质即可得出结论;
(2)此题根据△ABC中∠A为锐角与钝角分为两种情况解答.
(2)此题根据△ABC中∠A为锐角与钝角分为两种情况解答.
解答: 解:(1)∵AD=2.2cm,AC=3.7cm,
解:(1)∵AD=2.2cm,AC=3.7cm,
∴CD=3.7-2.2=1.5(cm).
∵∠C=90°,
∴点D到AB边的距离=CD=1.5(cm).
故答案为:1.5;
(2)如图1,当AB的中垂线MN与AC相交时,
∵∠AMD=90°,
∴∠A=90°-50°=40°,
∵AB=AC,
∴∠B=∠C=
=70°;
如图2,当AB的中垂线MN与CA的延长线相交时,
∴∠DAB=90°-50°=40°,
∵AB=AC,
∴∠B=∠C=
∠DAB=20°.
故答案为:70°或20°.
 解:(1)∵AD=2.2cm,AC=3.7cm,
解:(1)∵AD=2.2cm,AC=3.7cm,∴CD=3.7-2.2=1.5(cm).
∵∠C=90°,
∴点D到AB边的距离=CD=1.5(cm).
故答案为:1.5;
(2)如图1,当AB的中垂线MN与AC相交时,
∵∠AMD=90°,
∴∠A=90°-50°=40°,

∵AB=AC,
∴∠B=∠C=
| 180°-∠A |
| 2 |
如图2,当AB的中垂线MN与CA的延长线相交时,
∴∠DAB=90°-50°=40°,
∵AB=AC,
∴∠B=∠C=
| 1 |
| 2 |
故答案为:70°或20°.
点评:本题考查的是角平分线的性质,熟知角的平分线上的点到角的两边的距离相等是解答此题的关键.

练习册系列答案
相关题目
在a-(b-c)=a-b+c,4+x=9,6=2πr,3x+2y中等式的个数为( )
| A、1个 | B、2个 | C、3个 | D、4个 |
把分式方程
-
+1=0去分母可得( )
| 3 |
| x+5 |
| x-3 |
| x-5 |
| A、3x-5)-(x-5)(x-3)+1=0 |
| B、3x-5+(x+5)(x-3)+(x+5)(x-5)=0 |
| C、3(x-5)-(x+5)(x-3)+(x+5)(x-5)=(x+5)(x-5) |
| D、3(x-5)-(x+5)(x-3)+(x+5)(x-5)=0 |
 小李家住房的结构如图所示,小李打算把卧室和客厅铺上木地板,请你帮他算一算,他至少需买多少平方米的木地板( )
小李家住房的结构如图所示,小李打算把卧室和客厅铺上木地板,请你帮他算一算,他至少需买多少平方米的木地板( )| A、12ab | B、10ab |
| C、8ab | D、6ab |
 在△ABC中,O为∠CAB和∠CBA的角平分线的交点,若∠AOB=120°,则∠C的度数为( )
在△ABC中,O为∠CAB和∠CBA的角平分线的交点,若∠AOB=120°,则∠C的度数为( )| A、120° | B、60° |
| C、50° | D、30 |
 如图,已知∠AOB=a外有一点P,画点P关于直线OA的对称点P′,再作点P′关于直线OB的对称点P″.
如图,已知∠AOB=a外有一点P,画点P关于直线OA的对称点P′,再作点P′关于直线OB的对称点P″.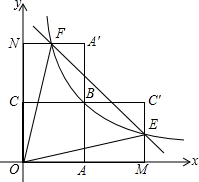 如图,四边形OABC是面积为4的正方形,反比例函数
如图,四边形OABC是面积为4的正方形,反比例函数