题目内容
13.“校园安全”受到全社会的广泛关注,绵阳市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了如图两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)接受问卷调查的学生共有60人,扇形统计图中“基本了解”部分所对应扇形的圆心角为90°;
(2)请补全条形统计图;
(3)若该中学共有学生3000人,请根据上述调查结果,估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数;
(4)若从对校园安全知识达到了“了解”程度的3个女生和2个男生中随机抽取2人参加校园安全知识竞赛,请用树状图或列表法求出恰好抽到1个男生和1个女生的概率.
分析 (1)由了解很少的有30人,占50%,可求得接受问卷调查的学生数,继而求得扇形统计图中“基本了解”部分所对应扇形的圆心角;
(2)由(1)可求得了解的人数,继而补全条形统计图;
(3)利用样本估计总体的方法,即可求得答案;
(4)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与恰好抽到1个男生和1个女生的情况,再利用概率公式求解即可求得答案.
解答 解:(1)∵了解很少的有30人,占50%,
∴接受问卷调查的学生共有:30÷50%=60(人);
∴扇形统计图中“基本了解”部分所对应扇形的圆心角为:$\frac{15}{60}$×360°=90°;
故答案为:60,90°;
(2)60-15-30-10=5;
补全条形统计图得: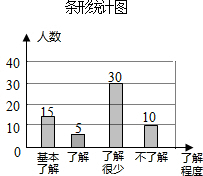
(3)根据题意得:3000×$\frac{15+5}{60}$=1000(人),
则估计该中学学生中对校园安全知识达到“了解”和“基本了解”程度的总人数为1000人;
(4)画树状图得:
∵共有20种等可能的结果,恰好抽到1个男生和1个女生的有12种情况,
∴恰好抽到1个男生和1个女生的概率为:$\frac{12}{20}$=$\frac{3}{5}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
3.下列图形中,是中心对称图形但不是轴对称图形的是( )
| A. | 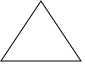 | B. | 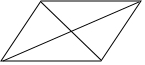 | C. | 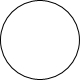 | D. |  |
4.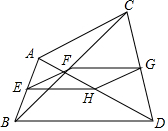 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
(1)求证:四边形EFGH为平行四边形.
(2)当AC=BD时,求证:四边形EFGH为菱形.
 如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.
如图,在四边形ABDC中,E,F,G,H分别为AB,BC,CD,DA的中点,并且E,F,G,H四点不共线.(1)求证:四边形EFGH为平行四边形.
(2)当AC=BD时,求证:四边形EFGH为菱形.
8.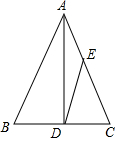 如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
 如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )
如图,已知AD是等腰△ABC底边BC上的高,sinB=$\frac{4}{5}$,点E在AC上,且AE:EC=2:3,则tan∠ADE=( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{5}$ |
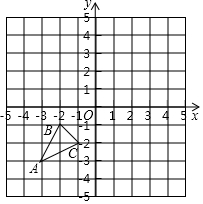 如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐标系上三点.
如图,已知A(-3,-3),B(-2,-1),C(-1,-2)是平面直角坐标系上三点.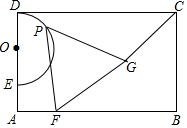 如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.
如图,E是矩形ABCD边AD上一点,以DE为直径向矩形内部作半圆O,AB=4$\sqrt{3}$,OD=2,点G在矩形内部,且∠GCB=30°,GC=2$\sqrt{3}$,过半圆弧(含点D,E)上动点P作PF⊥AB于点F.当△PFG是等边三角形时,PF的长是4或6.