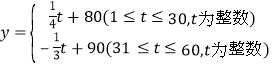Question

【题目】如图，四边形ABCD中，点E在边CD上，连结AE、BE.给出下列五个关系式：①AD∥BC；②DE=CE；③∠1=∠2；④∠3=∠4；⑤AD＋BC=AB．将其中的三个关系式作为题设，另外两个作为结论，构成一个命题．

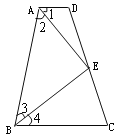
⑴用序号写出一个真命题（书写形式如：如果×××，那么××）；并给出证明；

⑵用序号再写出三个真命题（不要求证明）

Answer 1

【答案】（1）如果①②③，那么④⑤，证明见解析（2）如果①②④，那么③⑤; 如果①③④，那么②⑤;如果①③⑤，那么②④

【解析】

（1）如果①②③，那么④⑤．过E点作EF∥AD，与AB交于点F，根据平行线的性质推出EF为梯形ABCD的中位线，根据平行线的性质和等量代换，即可推出∠4=∠3，AB=2EF，通过2EF=AD+BC，即可推出AB=AD+BC，（2）根据真命题的定义，写出命题即可．

（1）如果①②③，那么④⑤.

证明：延长AE交BC的延长线于F,

∵AD∥BC,∴∠ADE=∠FCE,又∵∠AED=∠CEF，DE=EC，∴△ADE≌△FCE．∴AD=CF，AE=EF．∵∠1=∠F，∠1 =∠2，∴∠2=∠F,∴AB=BF,∴∠3=∠4,∴AD+BC=CF+BC=BF=AB．

（2）如果①②④，那么③⑤; 如果①③④，那么②⑤;如果①③⑤，那么②④.