Question

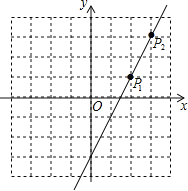
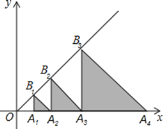
【题目】如图，△A1B1A2，△A2B2A3，△A3B3A4，…，△AnBnAn+1都是等腰直角三角形，其中点A1、A2、…、An在x轴上，点B1、B2、…、Bn在直线y=x上，已知OA2=1，则OA2015的长为____．

Answer 1

【答案】

【解析】

根据△A1B1A2为等腰直角三角形，所以A1B1OA2，A1B1=A1A2，然后根据等腰直角三角形斜边上的高等于斜边的一半求出A1B1、A1A2，同理求出A2B2，然后根据变化规律写出即可．

因为△A1B1A2为等腰直角三角形，所以A1B1OA2，A1B1=A1A2，又因为点B1在直线y=x上，所以OA1= A1B1，故OA1= A1A2，即点为OA2的中点，又因为OA2=1，所以A1B1=A1A2= 。因为△A2B2A3为等腰直角三角形，所以A2B2OA2，，所以A1B1∥A1B2，所以A1B1为△OA2B2的边A2B2上的中位线，所以A1B1=A1B2，即A2B2=2 A1B1，同理可证A3B3=2A2B2，同理可证AnBn=2An-1Bn-1，所以AnBn=2An-1Bn-1=2（2An-2Bn-2）==2n-2。当n=2014时，

A2014B2014=22014-2，因为△A2014B2014A2015为等腰直角三角形，所以A2014A2015=A2014B2014=22014-2且A2014B2014OA2015因为点B2014在直线y=x上，所以OA2014= A2014B2014所以，OA2015=2A2014A2015=222012=22013故本题正确答案为22013。