题目内容
1)问题发现
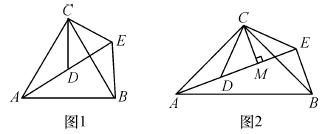
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.
(1)①60°;②AD=BE.
(2)∠AEB=90°;AE=2CM+BE.
理由:∵△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,
∴AC=BC,CD=CE,
∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
∴△ACD≌△BCE,
∴AD=BE,∠BEC=∠ADC=135°,
∴∠AEB=∠BEC-∠CED=135°-45°=90°.
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM=DM=ME,∴DE=2CM.
∴AE=DE+AD=2CM+BE.

练习册系列答案
相关题目
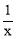 有意义,x的取值范围满足( )
有意义,x的取值范围满足( ) ,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.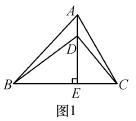

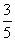 B.
B.  C.
C. 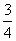 D.
D. 
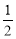 B.-
B.-